Among the 92 elements from hydrogen to uranium, helium is unique in not having a universally characteristic isotope ratio. Various mixtures of helium from three primary sources produce He-3/He-4 ratios over a six orders-of-magnitude range. The primary sources are: primordial, radiogenic, and cosmogenic. The concentrations of He-3 in many minerals, sediments, and volcanic provinces indicate that conventional geologic age assignments are grossly inflated, since these concentrations are orders-of-magnitude greater than may be expected on the basis of laboratory measurement of diffusion rates.
Attempts to account for the He-4 in Earth's atmosphere on the basis of diffusion of radiogenic helium from the crust and thermal loss to outer space yield unreasonable models. This consideration, and observations concerning non-thermal escape processes first made during the 1970s, have led to the conclusion that helium escape from Earth is largely by non-thermal processes. Of the seven such processes that have been identified, the greatest loss appears to be in a polar "wind" of ions accelerated along open lines of magnetic field in the regions surrounding Earth's magnetic poles.
INTRODUCTION
Among the chemical elements that exist with significant abundance in the Solar System, helium is unique in that it has the smallest ratio of minimum to maximum isotope abundance among the 86 elements that have more than one isotope (various numbers of neutrons in the nucleus). As given in the standard tables of relative isotope abundance, the Helium-3/Helium-4 ratio is only 0.000,00137 (1.37´10-6). Standard helium is 99.999,863% He-4, and 0.000,137% He-3. [1] These data refer to helium in Earth's atmosphere. The nearest competitors for lowest isotope abundance ratio among the 92 elements are calcium with 0.004% abundant Ca-46, and uranium with 0.0055% abundant U-234. [2]
VARIATION OF HELIUM ISOTOPE RATIO
The isotope ratios of an element generally are a physical characteristic that is independent of the source from which a sample may be obtained. [3] Helium is a dramatic exception.
In lava samples taken October 1-7, 1996, from various locations on Lohi seamount, an active submarine volcano situated about 30 km south of the island of Hawaii, the He-3/He-4 ratio R varied from 11.5 to 25.3 times the 1.37´10-6 characteristic value for air (RA). [4] Stepwise heating of limestone from a quarry in Kunnekulle, Sweden, released helium with R/RA ratios from 0.22 at 410°C, to 8.25 at 796°C just below fusion, and 22.7 at fusion. [5] Additional significant values of R/RA are listed in Table 1.
The R/RA values cited in Table 1 cover a range of over 25,000 from terrigenous sediment to Lohi seamount. It is fully evident that helium does not have a characteristic isotope ratio, as do the other chemical elements. A general characteristic of volcanic regions is that He-3/He-4 ratios in the rocks are similar in the central area, regardless of lithology and presumed eruption age; and decrease with distance away from the central area. [6] These unique features indicate that terrestrial helium comes from different sources, each with a distinct characteristic isotope ratio.
SOURCES OF HELIUM
Helium has three basic sources: primordial (initial creation), radiogenic (a product of radioactive decay), and cosmogenic (a product of nuclear reactions initiated by cosmic radiation). Elements that exist as a direct consequence of initial creation would be expected to have characteristic isotope ratios, with due allowance for minor changes that could have occurred since creation due to the slight changes that may have developed in some samples as the result of the dependence of diffusion rate and chemical reaction rate on atomic mass. The primordial He-3/He-4 ratio may be designated as RP. Unfortunately, no sample of helium has become available that can with 100% confidence be considered as primordial.
On the basis of geological considerations an estimate of (RP/RA) @ 73 has been suggested. [33] Excluding the items that may represent cosmogenic helium, the data in Table 1 indicate that (RP/RA) ³ 25. A theoretical estimate from Hot Big Bang cosmology suggests primordial (He-3/He-4) @ 10-4, about 73 times RA. [34] Since He-3 is in a higher energy state than He-4 (14.9 vs 2.3 MeV Mass Excess), matter that is the result of a supernova might have a lower (He-3/He-4) ratio (available energy is reduced in natural processes). We must keep in mind that Big Bang cosmology and the role of supernovae are highly speculative, and their specifications do not necessarily describe matter that appeared in an ex nihilo creation.
Analysis of the isotope abundances of the light elements may provide a clue concerning a probable value for RP. None of the first 21 elements in the periodic table, hydrogen through scandium, for which the most abundant isotope is even-numbered has an isotope of lower odd number, with the exception of helium. [35] He-3 is the only stable isotope with more protons than neutrons. These relationships strongly support a speculation that primordial helium did not initially contain He-3.
One source of radiogenic He-3 is the daughter-product of radioactive H-3 (tritium). Since tritium has a 12.33 year half-life, 50 years after the instant of primary primordial creation 94% of the H-3 created would have converted to He-3. Consequently He-3 produced from primordial H-3 may be considered as primordial helium. Hydrogen is 0.015% H-2. Since odd-numbered isotopes tend to be lower in abundance than associated even-numbered isotopes, it is reasonable to presume that in an instant of primordial creation any H-3 created was with abundance <0.015%. If the present cosmic-ray ratio of H/He, which is at least four, [36] represents the primordial H/He ratio, 70 years after Creation the He-3/He-4 ratio probably would have been less than 0.0006 (4´0.015%), and less than 430RA.
RADIOGENIC HELIUM
The major source of terrestrial helium appears to be from the ongoing transformation of heavy elements into lead. For every atom of lead derived from Uranium-238, or Uranium-235, or Thorium-232, there is produced 8, or 7, or 6 atoms, respectively, of He-4. A small amount of He-4 is also produced in the relatively rare spontaneous fission of radioactive heavy elements. Radiogenic helium is 100% He-4.
According to the best estimates for the composition of Earth's crust there is a 1.9´1014 kg inventory and a 2.5´106 kg annual production of He-4. [37] If there has been no loss to outer space, this inventory corresponds to about 80 million years of radiogenic accumulation. If the mass of planet Earth (the "foundation" of the earth, as the term "earth" is defined in Genesis 1:10) was created less than 10,000 years ago, these considerations together with the terrestrial data in Table 1 require speculation that at least two types of primordial helium were produced in the initial creation: one with RP/RA >40, and one with RP/RA <0.001.
The data in the CRC Handbook of Chemistry and Physics specify Earth's atmosphere to have 5.136´1018 kg total mass, 5.24´10-6 volume fraction of helium, and a molecular weight average of 28.57. According to these data the atmosphere contains 3.8´1012 kg of helium. To produce this amount of helium by the radioactive decay in the crust would require over 1.5 million years. Additional accumulation time would be required to account for loss from the atmosphere into outer space.
COSMOGENIC HELIUM
Helium produced on Earth by cosmic rays, and helium that comes to Earth from outer space, can be classified together as cosmogenic helium. Helium comes from outer space in the solar wind, and in meteoroids and interplanetary dust. Both He-3 and He-4 are produced in the breakup of atoms struck by cosmic-ray particles, and from nuclear reactions with the neutrons and muons produced by such breakup. [38] Production of helium by cosmic radiation is limited to the atmosphere and the top few meters of Earth's surface. [39] Estimates of cosmogenic helium production at Earth's surface are in the order of 104 atoms per cm2 of Earth surface per year. [40] Since the estimated production by radioactivity within the crust averages 7.4´1013 atoms per cm2 of surface per year, [41] the quantity of helium produced by cosmic radiation is a relatively negligible consideration. For meteoroids and cosmic dust that have no atmospheric shielding, production by cosmic radiation is a major consideration.
With interplanetary dust accumulating on Earth at the rate of ~4´104 tons/yr, [42] and an average He-3 content of 6.8´1014 atoms/gram, [43] the He-3 accumulation to Earth via interplanetary dust (IDP) is 136 g/yr. For an IDP R/RA @ 200 (see Table 1) this represents about 700 kg/yr of He-4, which is negligible compared with 2.5´106 kg/yr from radioactivity in the crust.
Since helium in the solar wind is ionized, Earth's magnetic field provides a shield that diverts a large portion of the solar wind helium from striking the surface. [44] As may be expected, the contribution from solar wind, together with that from IDP and cosmic-ray production is negligible in comparison with the production from radioactivity in the crust.
It is of passing interest to note that if the only sources of atmospheric helium had been radiogenic and cosmogenic, at present estimated rates, the atmospheric He-3/He-4 ratio would be in the vicinity of only 5% of the presently observed value. [45]
HELIUM-3 CONSTRAINTS ON GEOLOGICAL AGE
Since helium forms chemical bonds only in rare cases, and since it has only two orbital electrons; it diffuses relatively rapidly through a host mineral, and concentrations of He-3 above that in the surrounding medium should dissipate rapidly. The dissipation of a localized high R helium is analogous to the dissipation of a drop of dye on a large surface of water that has been tinted lightly with the same color. The concentration of He-3 atoms becomes distributed among an increasingly larger number of He-4 atoms, as the concentration of dye molecules become distributed in an increasingly larger number of water molecules. Any radioactive material that might be in the sediment would contribute only He-4, and increase the rate at which R is reduced.
In a report on He-3/He-4 ratios in Central North Pacific pelagic clay sediment, K.A. Farley (1995) noted that "Laboratory diffusion measurements extrapolated to sea-floor temperatures predict complete diffusive loss of 3He from IDP magnetite grains in <107 years after fallout." [46] The extraterrestrial data in Table 1 establish an upper boundary for R from which diffusion to an indistinguishable background level would be expected in <107 years. Yet the 1360-1365 cm interval of sediment core LL-44-GPC-3 has R/RA = 150, and an assigned geologic age of 45.18 Myr.
Farley's resolution of the dilemma is in proposing that the natural diffusivity in IDP is several orders-of-magnitude less than indicated by laboratory determinations. A simpler, more reasonable conclusion is that conventional geological age dating is incorrect that Core LL-44-GPC-3 is a sample of post-biblical-Flood sediment that accumulated <5500 years ago. [47] Farley's treatment of the data indicates that during the Quaternary, ocean sediment accumulated in the order of ten times faster than throughout the preceding 65 millions years of the Tertiary. Restricting "Tertiary" to the early portion of post-Flood time produces a more reasonable pattern of sediment accumulation rate. The 150 value for R/RA in the 1362 cm vicinity of Core LL-44-GPC-3 may indicate sediment deposit associated with passage of Earth through a region of interplanetary dust and meteoroid concentration.
Another indication that geological age assignments are grossly inflated is provided by helium in diamonds. In reporting their investigations of helium in diamonds, R.C. Wiens et al. (1994) note that "Measured and extrapolated effective 4He diffusivities at 1200°C are ... much higher [5-10 orders of magnitude] than ... required for quantitative helium retention over diamond ages"; "Bulk retention of trapped mantle helium over the age of most diamonds (>1 Ga) would require effective diffusion coefficients at least several orders of magnitude lower than that inferred for the cosmogenic helium component at 1200°C, typical of mantle temperatures." [48]
The remarkable similarity of helium isotope ratios (R/RA = 6.1±0.7 to 6.65±0.25) of volcanics in the Massif Central (France), the Eifel (Germany), the Spitsbergen (Arctic Ocean), and the Kapfenstein (Austria) Cenozoic volcanic provinces of Europe, regardless of geologic age assignments ranging from 3.5 thousand to ten million years, [49] taken together with the high diffusivity of He-3, is further indication that conventional geological age assignments are vastly inflated. Any mineral for which the He-3/He-4 ratio is markedly greater than that for the surrounding area, and that has a geologic age assignment in the millions-of-years range, is evidence for orders-of-magnitude discrepancy between real time and the conventional age assignment. As was already noted above, due to the high diffusivity of helium a concentration of relatively high R will blend together with a lower concentration in the surrounding area. The higher diffusivity of He-3 with respect to He-4 will augment the rate at which this blending occurs.
An analysis of olivine and clinopyroxine surface samples from the Bismarck Archipelago of Papua, New Guinea, gave cosmogenic He-3 concentrations that could be generated in 2.5-16 thousand years at an estimated present cosmogenic He-3 production rate (63 atoms per gram per year at sea-level on the equator). [50] An estimate that is uncertain within the range 2.5-16 kyr is in satisfactory agreement with formation of these islands since the Genesis Flood. [51]
According to Farley (1995), [52] He-4 concentrations in a 23 m length of central North Pacific pelagic clay core presumed to extend to ~72 Ma ago, are up to two orders-of-magnitude below predictions based on geological age assignments. The He-4 concentrations in this core decrease with depth, rather than increasing as would be expected on the basis of helium production and diffusion over the assigned age of core segments. Uranium concentration values reported in the source of the data on this core [53] also decrease with depth, exhibiting minor variations about a representative constant He/U ratio. From my perspective, the data are most readily explained by deposition over a few thousand years with sediment that has a U-He age characteristic which does not relate to the time of deposition.
Authors and editors are naturally inclined to, and are under pressure to, publish material that is readily understandable from the perspective of the prevailing concepts that presume geological features represent gradual overall development over millions of years. The appearance in the professional literature of the examples cited in this section indicates that there is a solid scientific basis for reconsidering the prevailing concepts related to geologic time.
LOSS OF HELIUM TO OUTER SPACE
An understanding of the helium content of the atmosphere must take into consideration the processes by which helium is lost to outer space. Representing the flux of the ith sort of atoms to outer space per unit area of surface by iF,
iF = in x if, (1)
with in the number of the ith sort of atoms per unit volume at the elevation for which determination is made, and if a factor with units of velocity that specifies the portion of these atoms that have an outward component of velocity equal to or greater than the escape speed vesc.
vesc = [2GM/r]½, (2)
with G the universal constant of gravitation, M the mass of Earth, and r the distance from Earth-center for which v esc is specified.
There are three types of process by which an atom may acquire sufficient speed to escape Earth's gravitation: (1) ionization and subsequent acceleration in electric fields, particularly in the regions around the magnetic poles; [54] (2) collisions that transfer energy from ions in the solar wind, or atoms that have been ionized by ultraviolet light; and (3) the high-energy portion of the thermal energy distribution (Jeans escape). [55] Jeans flux has been estimated to account for only about 1/6 of the helium loss from Earth's atmosphere. [56] Such estimates should be accepted with caution, since they may be derived from an assumption of helium equilibrium in the atmosphere, rather than actual physical measurements.
Since a quantitative estimate can be made readily for proposed Jeans flux, and even crude direct estimates have not been available for loss by ion acceleration and nonthermal collision interactions, treatment of atmospheric helium dynamics has usually featured Jeans flux. [57] For Jeans flux the appropriate if factor in Equ. (1) above, ifth, is
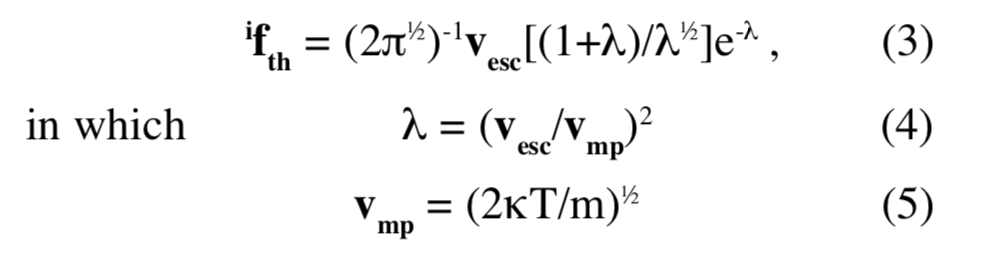
with vmp = most probable velocity, k = Boltzman's gas constant, T = absolute temperature in °K, and m = mass of the molecule. [58]
The concentration in the region from which escape to space is evaluated, in, may be a more significant factor in Equation (1) than if, the fraction of atoms that escape from that region. With a concentration gradient from Earth's surface to outer space, diffusion considerations would be the dominant factor in the establishment of in. The Jeans flux for the portion of in that have sufficient energy to escape the gravitational field is based on the Maxwell-Boltzman energy distribution function which is strictly valid only for an equilibrium state within a confined region, regardless of whether that region is defined by physical boundaries. Thus if there is escape, the Jeans flux provides at best only a first approximation to the actual portion of in that flow outward per unit of time as a consequence of energy acquired through thermal interaction. [59]
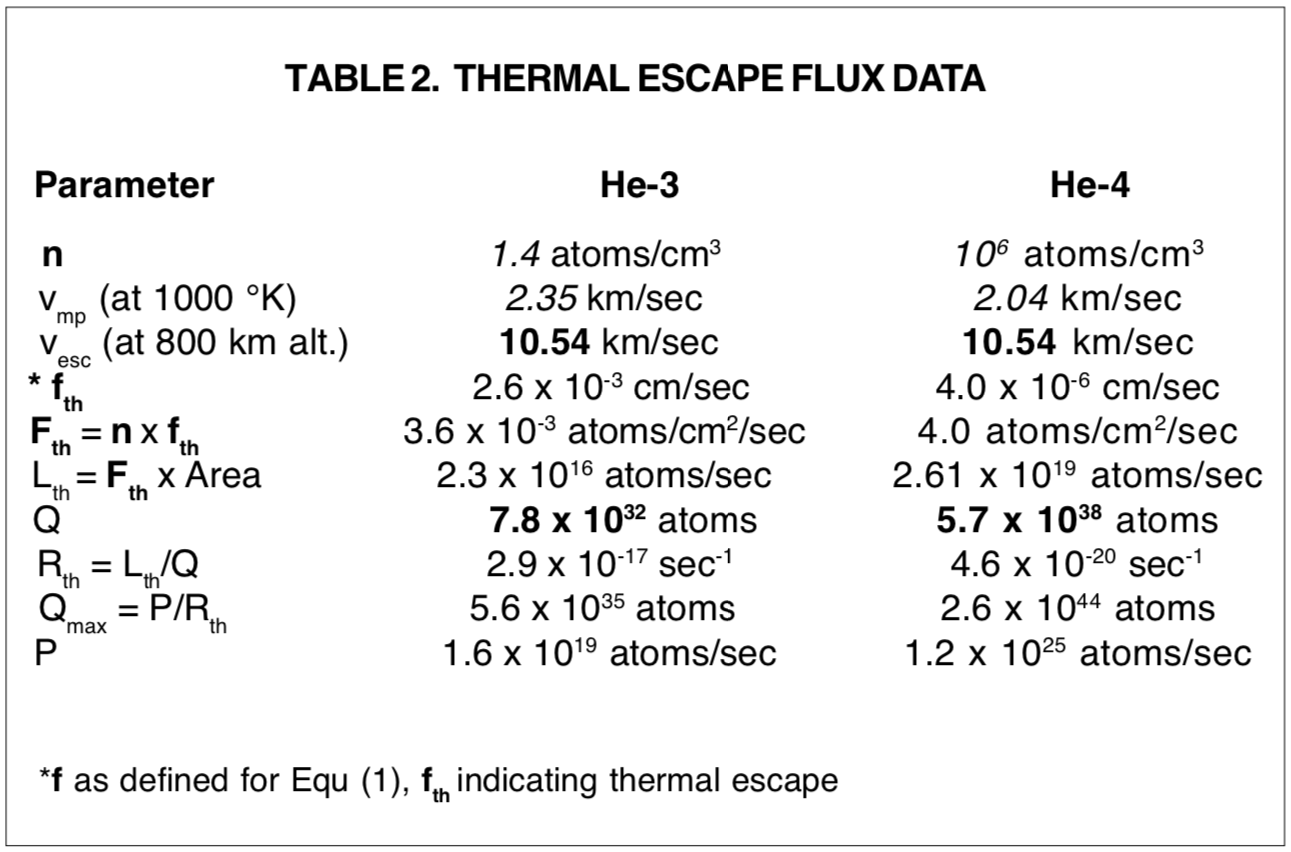
Table 2 is a tabulation of Jeans flux parameters for atmospheric helium at 800 km altitude (radius 7171 km from the center of Earth) and 1000°K. These temperature and altitude values were chosen from Figures 4 and 5 of the Astronomical Constants section of the CRC Handbook of Chemistry and Physics. [60] Values estimated or calculated from estimated values are shown in italics. Values measured or calculated from easured values are in bold face. All other values are from Jeans thermal flux escape calculations. The surface area of a sphere of 7171 km radius is 6.46´1018 cm2. For the production, P, of He-4 at equilibrium concentration, Qmax, the value 1.2´1025 atoms/sec for radiogenic production in the crust is used.
An estimation of the equilibrium concentration, Qmax, for He-3 may be obtained from noting that for both He-3 and He-4
Q = Qmax (1 - e-Rtht). (6)
He-4 Qmax may be determined using for P the He-4 production in the crust, assuming that at equilibrium thermal escape from the atmosphere will equal diffusion from the crust into the atmosphere, and diffusion from the crust is equal to production in the crust. The 2.6´1044 atoms value in Table 2 was calculated on this basis. Simultaneous equations may be obtained from Equ. (6), using the present inventory for Q, the appropriate respective values for Rth, and an unspecified time tp (present) for t. Eliminating tp between the two equations produces an equation that may be solved for He-3 Qmax to obtain the 5.6´1035 atoms value in Table 2.
The reciprocal of Rth as defined in Table 2 is the exponential relaxation time, Tr the time in which an exponential term multiplies or divides e-fold (2.718 times). Table 3 lists significant time intervals for evaluation of the thermal escape model. The reader should keep in mind that these time intervals are hypothetical, and are based on the assumption that the atmosphere at one time did not contain any helium.
For a crustal production rate 1/10 as great as that based on uniform distribution of U and Th (3.75´1031 atoms He-4 per year), Qmax would be 2.6´1043 atoms for He-4, and 5.6´1034 atoms for He-3; and the time for reaching the present Q would increase from 1.5 million years to 15 million years.
In the same way that Qmax for He-4 was derived from a value for the production rate, the production rate for He-3 may be derived from a value for its Qmax. The time-projection of He-3/He-4 ratio in the atmosphere, according to the thermal escape model, indicates relatively rapid (i.e., compared with He-4) accumulation of He-3 to an equilibrium level which is about 1/450 of that which would be expected if the two isotopes had equal probability for loss to outer space (quotient of Equilibrium and "Time-Zero" ratios of Table 4).
The "Time-Zero" value is obtained from recognition that in a backward approach to the limit of time-zero, the concentration ratio approaches the production ratio. It must be kept in mind that these considerations assume constant annual diffusion into the atmosphere of the amount of He-4 that has been estimated for the present yearly radiogenic production of helium in Earth's crust. In 10 billion years the He-4 production in the crust is projected to be about half its present rate. Consequently, conclusions from the foregoing analysis should not be extended beyond a range of about two billion years.
BOUNDARY-LIMITED THERMAL MODEL FOR ATMOSPHERIC HELIUM
The extreme disequilibrium, and the unrealistic time-interval projections of the Jeans escape model as developed in the foregoing paragraphs, make the usefulness of this model highly questionable. Before discarding it, the possibility for modifying basic assumptions sufficiently to make the model more attractive should be investigated. Modification of these assumptions to the extreme extent I think might be justified yields what may be designated as the Boundary-Limited Thermal Model. For this model, He-4 production is presumed to be 1/10 of the value obtained from assumed uniform distribution of thorium and uranium from the surface to the base of Earth's crust. And the kinetic temperature of the escape region is presumed to be 1500°K, the upper extreme of a range of uncertainty that may be inferred from Figure 4 in the CRC Handbook of Chemistry and Physics. [61] The Jeans escape function is so sensitive to temperature that this 500° increase produces an increase of about 5400-fold in the thermal escape flux. The specifications of this model are given in Table 5, with presumed values in italics, and measured values in bold-face.
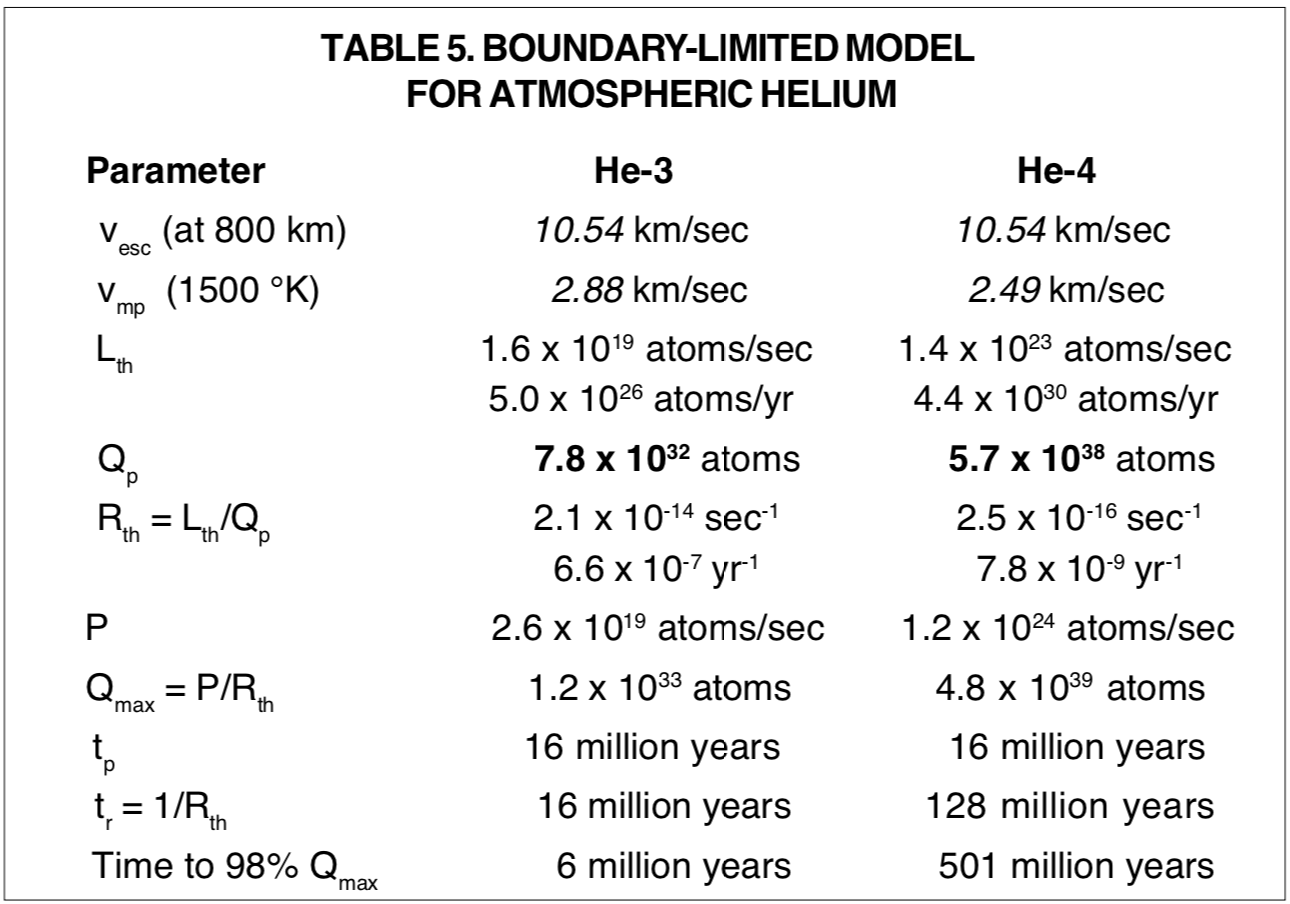
Although the time values of the Boundary-Limited Thermal Model are all within the usually accepted 4.6 billion years for the age of Earth, the extreme assumptions that are necessary to accomplish this make the best accomplishment of Jeans escape modeling to be inducement to search for nonthermal mechanisms by which helium might escape Earth's atmosphere.
NONTHERMAL ESCAPE
Before space exploration provided direct measurements of the gases in the exospheres (regions from which escaping particles originate) of Earth and the other inner planets of the Solar System, treatment of escape from the upper levels of an atmosphere seemed fairly straightforward. [62] In the data that became available from space missions were surprises that have considerably altered our understanding of atmospheric stability. [63] It is now recognized that there are probably seven nonthermal processes [64] by which gases may escape a planetary atmosphere (see Table 6). Five of these seven involve atoms in an ionized state to which the Jeans escape does not apply. Ion escape at the magnetic poles where there is no transverse acceleration of a moving charged particle is considered by Chamberlain and Hunten [67] to be the principal means by which helium escapes from Earth. A recent issue of Physics Today[68] has a space-vehicle photograph of the solar ultraviolet light scattered by the ionized helium surrounding Earth. This photo indicates that a distinct concentration of helium extends over a region about three times the diameter of Earth (elevation about 8000 miles, or 13,000 km, above Earth surface).
There is need for a quantitative model that enables determination of the extent to which the rate of helium loss to outer space is limited by diffusion, rather than by the processes for attaining escape velocity. According to one estimate, the loss of hydrogen to outer space is determined by the diffusion to the exosphere. [69] If all the atoms of a specific type in a layer of the exosphere are eventually lost to outer space, the population gradient of that type in the underlying layers will adjust to a level that supports a loss rate to outer space that is equal to the rate of input by diffusion, making diffusion the limiting factor in the establishment of a loss rate.
CONCLUSIONS
One firm conclusion which can be made is that the dynamics of helium isotope concentrations in Earth's crust and atmosphere are highly complex, and beyond adequate treatment with a simple model. Treatment of helium in the atmosphere as if thermal considerations (Jeans escape) account for the major loss to outer space produces a model that specifies a high degree of disequilibrium, and indicates an equilibration time within a range between half a billion years and greater than the half-life of uranium, even greater than the proposed age of the Solar System. It is evident that Jeans escape modeling does not relate adequately to physical reality; and that, contrary to claims frequently made in creationist literature, it does not provide significant evidence in support of (or contradictory to) a young-earth viewpoint.
There is ample evidence that consideration must be given: (a) to diffusion flow of helium to the region from which loss to outer space occurs; (b) to loss from ion acceleration in the regions around the magnetic poles; (c) and to loss from energy gain in collision with solar wind atoms and atmosphere atoms that have been elevated to a high energy state by ultraviolet radiation.
There is an option of considering the primordial creation of the matter in Earth's crust and atmosphere to have been coincident (within one week) with the placement of organic life on the planet. In this option the helium isotope distribution in the crust, the atmosphere, and areas of volcanic activity on the surface should be recognized as requiring the creation of at least two types of helium, each with a distinct primordial He-3/He-4 ratio, differing by several orders-of-magnitude. This seems unlikely. There is no evidence for the creation of any other element in this manner, and no evidence of need for helium to be so different from all other elements. The present helium content of Earth's atmosphere may not be any more explainable than is the present nitrogen and oxygen content.
With the data at hand we should at least be able to predict trends in atmospheric helium abundance and isotope ratio. An unexpected conclusion from this study is the low rates that may be anticipated for these trends, if thermal escape is a dominant factor. According to the "Boundary-Limited Thermal Model" He-4 will not reach equilibrium level in the atmosphere until around 400 million years in the future! The simplistic assumptions on which the model is based may not be expected to be applicable over so long a time period. The question of the rate of loss of helium to outer space remains an enigma. Several alternatives are possible.
One clear implication of the helium isotope data in the professional literature is that conventional geologic age assignments may be grossly inflated. The implications of laboratory-determined He-3 diffusion rates are persistently ignored in favor of conventional geologic age assumptions. Any mineral for which the He-3/He-4 ratio is conspicuously higher than for the surrounding minerals or area, is prime evidence that the host igneous or sedimentary formation was emplaced within the last few million years. On the basis of helium isotope ratio data, there is better scientific foundation for placing the formation of the Phanerozoic portion of the geologic column within the past 10,000 years than to extend it over 500 million years.
ACKNOWLEDGMENTS
In the preparation of this treatment, and in the development of the concepts presented, I have been assisted from discussions with Drs. Benjamin Clausen, Paul Giem, and Clyde Webster. Readers are greatly benefited by Dr. Giem's suggestions concerning preparation of the draft for publication. Appreciation is due unnamed reviewers for a wide range of clarifications in the final manuscript.
ENDNOTES
[1](a) Isotope data in this paper are taken from: Tuli JK. 1995. Nuclear Wallet Cards, 5th edition. Upton, NY: National Nuclear Data Center, Brookhaven National Laboratory; (b) also see Table of the Isotopes in: Lide DR, editor. 1994. Handbook of chemistry and physics. 75th edition. Boca Raton, FL: CRC Press.
[2]See Note 1. U-234 is radioactive (unstable) with a 2.455´105 year half-life. The 0.0055% abundance of U-234 is equal to the equilibrium ratio of U-234 to its parent U-238. Ninety-eight percent of this ratio would be attained by one million years after an isolated sample of U-238 was created.
[3]Small variations may occur in samples that have experienced thermal diffusion or chemical reaction, since the lighter isotopes move slightly faster in these processes. Such variations are usually expressed in parts per thousand (per mil, or ). An isotope may be in excess of its standard value if it is a daughter of a radioactive parent and there has been a previous association with the parent element. E.g., primordial lead that has been associated with uranium will have enhanced ratios of the lead isotopes that are daughters of uranium.
[4]Hilton DR, McMurty GM, Goff F. 1998. Large variations in vent fluid CO2/3He ratios signal rapid changes in magma chemistry at Lohi seamount, Hawaii. Nature 396:359-362.
[5]Patterson DB, Farley KA, Schmitz B. 1998. Preservation of extraterrestrial 3He in 480-Ma-old marine limestones. Earth and Planetary Science Letters 163:315-325.
[6]Dunai J, Bauer H. 1995. Helium, neon, and argon systematics of the European sub-continental mantle: implications for its geochemical evolution. Geochimica et Cosmochimica Acta 59(13):2767-2783.
[18]Marty B, Tolstikhin I, Komensky IL, Niven V, Balaganskaya E, Zimmerman J-L. 1998. Plume-derived rare gases in 380 Ma carbonatite from the Koala region (Russia) and argon isotopic composition in the deep mantle. Earth and Planetary Science Letters 164:179-192.
[19]Patterson DB, Farley KA, McInnes BIA. 1997. Helium isotopic composition of the Tabar-Tanga-Feni island arc, Papua New Guinea. Geochimica et Cosmochimica Acta 61(12):2485-2496.
[21](a) Tedesco D, Nagao K, Scarsi P. 1998. Noble gas isotope ratios from historical lavas and fumaroles at Mount Vesuvius (southern Italy): constraints for current and future volcanic activity. Earth and Planetary Science Letters 164:61-78; (b) Farley KA, Neroda E. 1998. Noble gases in the earth's mantel. Annual Review of Earth and Planetary Sciences 26:189-218; (c) Anderson 1993 (see Note 10).
[23]Hilton DR, Hammerschmidt K, Teufel S, Friedrichsen H. 1993. Helium isotope characteristics of Andean geothermal fluids and lavas. Earth and Planetary Science Letters 120:265-282.
[24]Marty B, Pik R, Gezahegn Y. 1996. Helium isotope variations in Ethiopian plume lavas, nature of magmatic sources and limit on lower mantle contribution. Earth and Planetary Science Letters 144:223-237.
[26](a) Marcantonio F, Kkumar N, Stute M, Anderson RF, Seidl MA, Schlosser P, Mix A. 1995. A comparative study of accumulation rates derived by He and Th isotope analysis of marine sediments. Earth and Planetary Science Letters 133:549-555; (b) Marcantonio F, Higgins S, Anderson RF, Stute M, Schlosser P, Rasbury ET. 1998. Terrigenous helium in deep-sea sediments. Geochimica et Cosmochimica Acta 62(9):1535-1543.
[27]Patterson, Farley & Schmitz 1998 (see Note 5).
[29]Ballentine CJ, O'Nions RK, Coleman ML. 1996. A magnus opus: helium, neon and argon isotopes in a North Sea oilfield. Geochimica et Cosmochimica Acta 60(5):831-849.
[30]Data supplied by David Cornelius, Lead Chemist, U. S. Bureau of Land Management, Amarillo Field Office, Amarillo, Texas. The "Texas" helium field extends from southwestern Kansas into New Mexico.
[32]Verchovsky AB, Ott U, Begemann F. 1993. Implanted radiogenic and other noble gases in crustal diamonds from Northern Kazakhstan. Earth and Planetary Science Letters 120:87-102.
[33]O'Nions RK, Oxburgh ER. 1983. Heat and helium in the Earth. Nature 306:429-431.
[34]Burbidge G, Hoyle F, Narlikar JV. 1999. A different approach to cosmology. Physics Today 52(4):38-44.
[35]For Li, Be, B, F, Na, Al, P, Cl, K, and Sc the most abundant isotope is odd-numbered. Of these, Be, F, Na, Al, P, and Sc are monoisotopic. For Li and B the second-most abundant isotope is even-numbered, and lower Li-6 at 7.5% vs Li-7 at 92.5%; B-10 at 19.9% vs B-11 at 88.1%. For Cl and K the second-most abundant isotope is odd-numbered and higher Cl-37 at 24.23% vs Cl-35 at 75.77%; K-41 at 6.7302% vs K-39 at 93.2581%.
[36]Lide 1994, "Cosmic Radiation", Section 11: Nuclear and Particle Physics, p 155 (see Note lb).
[37]Lide 1994, "Astronomical Constants," Section 14 (see Note lb), provides the following data for Earth's crust: Total Mass 2.36´1022 kg; 8´10-3 mg/kg He; 9.6 mg/kg Th; 2.7 mg/kg U. Th-232 has a 1.405´1010 yr half-life, and produces 6 He-4 atoms per Th decay. U-238 has a 4.468´109 yr half-life, and produces 8 He-4 atoms per U-238 decay. U-235 is 0.720% of uranium, has a 0.7038´109 yr half-life, and produces 7 He-4 atoms per U-235 decay. The U-235 contribution brings the total He-4 atoms per U-238 decay to 8.04. The combined production from Th and U is 1.6´1010 He-4 atoms/yr kg, or 1.1´10-13 grams of helium per year per kilogram of crust. If the 9.6 and 2.7 mg/kg concentration estimates correctly represent the entire crust, the total He-4 production is 2.5´106 kg/yr, or 7.38´1013 atoms/yr per cm2 of surface.
[38]Lide 1994, "Cosmic Radiation", Section 11: Nuclear and Particle Physics (see Note lb).
[39]The attenuation depth e-fold rate is given as approximately 55 cm in basalt. At this rate the intensity is reduced to <3% in two meters. See: Cerling TE, Craig H. 1994. Cosmogenic 3He production rates from 39°N to 46°N latitude, eastern USA and France. Geochimica et Cosmochimica Acta 58:249-255.
[40](a) Cerling & Craig, 1994 (see Note 39); (b) Lal D. 1991. Cosmic ray labeling of erosion surfaces: in situ nuclide production rates and erosion models. Earth and Planetary Science Letters 104:424-439.
[44](a) Cowley SWH. 1995. The Earth's magnetosphere: a brief beginner's guide. EOS, Transactions of the American Geophysical Union 76(51):525-529; (b) Russell CT, editor. 1991. Venus aeronomy. Dordrecht, Boston, and London: Kluwer Academic Publishers (reprinted from Space Science Reviews 55:1-489).
[45]Assuming that equilibrium has been established so that the same amount of He-4 diffuses to the atmosphere per year as is generated in the crust, (He-3/He-4) = 136/(2.5´109) ´ 4/3 = 7.2´10-8 @ 5% ´ RA.
[47]Placing the date of the Flood at about 3400 B.C., according to 1 Kings 6:1; Exodus 12:40,41; Genesis 47:9; 25:26; 21:5; 11:10-26; with construction of Solomon's Temple in 970 B.C., and chronological data as specified in the Septuagint text. This limit would be extended from 5500 to between 10 and 15 thousand years with the interpretation proposed by Gerald Aardsma [1993. A new approach to the chronology of biblical history from Abraham to Samuel. El Cajon, CA: Institute for Creation Research. For a critique, see: Wood BG. 1993. Bible and Spade 6(4):97-114].
[54](a) Colin HL. 1997. Observations of aural ion outflow from the POLAR spacecraft. EOS, Transactions of the American Geophysical Union, Fall Meeting Supplement 78(46):F605; (b) Lockwood M, Moore TE, Waite (Jr.) JH, Chappell CR, Horwitz JL, Heelis RA. 1985. The geomagnetic mass spectrometer mass and energy dispersions of ionospheric ion flows into the magnetosphere. Nature 316:612-613; (c) Ghielmetti AG, Johnson RG, Sharp RD, Shelley EG. 1978. The latitudinal, diurnal, and altitudinal distributions of upward flowing energetic ions of ionospheric origin. Geophysical Research Letters 5:59-62; (d) Suess HE. 1987. Chemistry of the solar system. NY: John Wiley & Sons, p 95.
[55](a) Walker G. 1995. On the wings of Pegasus. Nature 378:333; (b) Fahr HJ, Shizgal B. 1983. Modern exospheric theories and their observational relevance. Reviews of Geophysics and Space Physics 21(1):75-124; (c) Shizgal BD, Arkos GG. 1996. Nonthermal escape of the atmospheres of Venus, Earth, and Mars. Reviews of Geophysics 34(4):483-505.
[59]The appropriate correction factor has been placed in the range 0.5-0.8. See: Hunten DM. 1982. Thermal and Nonthermal Escape Mechanisms for Terrestrial Bodies. Planetary and Space Science 30(8):773-783.
[67]Chamberlain & Hunten 1987, p 367 (see Note 63).
[68][Editor's news item]. Physics Today 53 (August), p 9.
[69]Shizgal BID, Arkos GG. 1996. Nonthermal escape of the atmospheres of Venus, Earth, and Mars. Reviews of Geophysics 34(4):483-505, specifically p 489.
Left: Ultraviolet image of the interaction of charged particles with the neutral gases of Earth's atmosphere. Right: Ultraviolet image of sunlight scattered from Earth's extended atmosphere of helium. Photographs courtesy of NASA (see http://image.gsfc.nasa.gov/). This article discusses the significance of helium isotope ratios in the atmosphere. This images were used in the cover and back cover of Volume 25 Number 2, 1998 of the Origins magazine.
