©Copyright 2018 GEOSCIENCE RESEARCH INSTITUTE
11060 Campus Street • Loma Linda, California 92350 • 909-558-4548

THE NATURE OF EVIDENCE FOR THE ACTIVITY OF SUPERNATURAL INTELLIGENCE, AS ILLUSTRATED BY POLONIUM RADIOHALOS
by
R. H. Brown
Yucaipa, California
ABSTRACT
The polonium isotopes that produce radiohalos do not have a pattern of isotope abundance ratios similar to that of the other naturally occurring 91 chemical elements. Instead, polonium radiohalos are limited to the isotopes produced by daughters of long-lived uranium and thorium parents. Moreover, polonium radiohalo abundances are not in the 1:1 ratio of radioactive daughter-product production. Their abundance ratios are more similar to the associated half-life ratios. This feature could indicate relative time of survival in transport from the point of origin, simultaneous deposition from a solution carrying isotopes in equilibrium, or a combination of these processes.
For many individuals, the rare occurrence of 164 microsecond Po-214 radiohalos and of radiohalos in diamonds are readily accounted for by presuming de novo, in situ fiat creation. Another model based on infusion of daughter-product solutions accounts for the incongruities in the direct creation model. The present limited knowledge of hydrothermal diffusion through crystal lattice planes, and of geochemistry at lattice imperfection and impurity sites does not provide an unquestionable selection between the two models for explaining polonium radiohalos. Either model is within the creation classification, the difference being the level at which basic activity of the Creator is presumed to have been manifest.
INTRODUCTION
How can a particular phenomenon be evidence for the activity of a supernatural intelligence? From the baffling intricate characteristics of atoms, to the amazing yet barely perceived dynamics of stellar galaxies; from the complex operation of a living cell, to the unexplained capabilities of the human mind; where can we find specific evidence for the activity of an all-encompassing intelligence, objective evidence for God?
Confronted with the reality of the material universe, with all its intricate complexity and delicately balanced interaction, it is logical to presume the existence of an all-encompassing intelligence as the Designer, Initiator, and Maintainer of the vast range of phenomena that we observe. In his epistle to the Romans, the Apostle Paul affirms that individuals who do not reach such a conclusion are "without excuse" (Rom. 1:19,20).
Ancient man tended to consider all physical phenomena as a direct manifestation of deity. For example: God in the sun; God, or perhaps another god, in the moon; god in the mountain; god in the sea; god in the tree; god in the lion. As knowledge increased, that which was considered to be a direct expression of deity has been pushed back to the level where understanding ceased. We now base our understanding of stars, geological formations, plants, and animals on the characteristics of the 92 different elements (kinds of atoms) and their compounds. However, the properties of these 92 basic elements and their compounds, and anything that cannot be explained on the basis of underlying phenomena, is considered by some individuals to be evidence of immediate and direct activity by the Intelligence who created and sustains the physical universe. Subsequent increased understanding may transfer the "evidence" to a simpler, more basic level, and foster an enlarged perception of the fundamental laws that were established by the Creator to maintain the universe.
An example of this progression to a more basic level is provided by the element lead. It is no longer necessary to postulate that God created lead in a mystifying wide variety of isotope ratios in various minerals. The range of lead isotope variation may be accounted for readily by mixing of primordial (from an initial creation event, whether a supernova explosion or a simple "God spoke" event) lead with lead produced by radioactive decay of uranium and thorium. This advanced understanding in no way diminishes the significance of atomic structure as evidence for design, creation, and maintenance by the Creator.
EXPECTATIONS CONCERNING PRIMORDIAL POLONIUM
The primary object of this paper is consideration of the evidence for the source of the element polonium. Each polonium atom contains 84 protons that determine its chemical characteristics. Eighty-four protons will not stay together in a nucleus unless they are accompanied by at least 106 neutrons. The number of accompanying neutrons may be as great as 134. The range of allowed neutrons gives polonium 29 isotopes (different forms which have the same chemical characteristics, but slightly different physical properties).
None of the 29 proton-neutron combinations in which polonium may be produced is stable. There is a spontaneous trend toward combinations that are stable. This trend is called radioactivity, because it was first observed in investigation of the element radium, which also is unstable. There is no known way to predict when an individual radioactive atom will convert to the next stage in the trend toward a stable proton-neutron combination; but it is possible to measure for a large number of atoms the statistical average of the time required for transition. The most convenient way to represent this average is known as half-life.[1] The most stable isotope of polonium Po-209, which has 125 neutrons has a half-life of 102 years. The least stable polonium isotope Po-212, which has 84 protons and 128 neutrons has a half-life of only 0.299 microseconds. Any Po-209 that was brought into existence in primordial creation (an initial creation event) would have diminished to about 1/1000 of its initial amount by 1000 years later.[2]
To anticipate what might be expected in the primordial composition of polonium, we can compare polonium with two other elements that, like polonium, may exist in a wide range of isotopes. Tin, with 38 isotopes, and tellurium, with 14 isotopes, are the best elements for indicating the primordial abundance ratios and half-life features that we might expect for polonium. Tellurium and polonium have similar chemical characteristics, and are classified as Periodic Table Column VIA (Chemical Abstracts Service notation) elements.
Figure 1 shows the relative nuclear binding energies of the isotopes of tin compared with isotope 118 arbitrarily set as 1.000. There is no binding energy data currently available for isotopes 135, 136, and 137. Ten of the 38 isotopes of tin are stable. The percentage relative abundance of these ten stable isotopes is given at the top of their respective bars in Figure 1. Logarithms (base 10) of the half-lives of the unstable tin isotopes are represented in Figure 2. The available data only permit determination of a minimum (150 nanoseconds) for the half-lives of tin 102, 135, 136, and 137.[3]
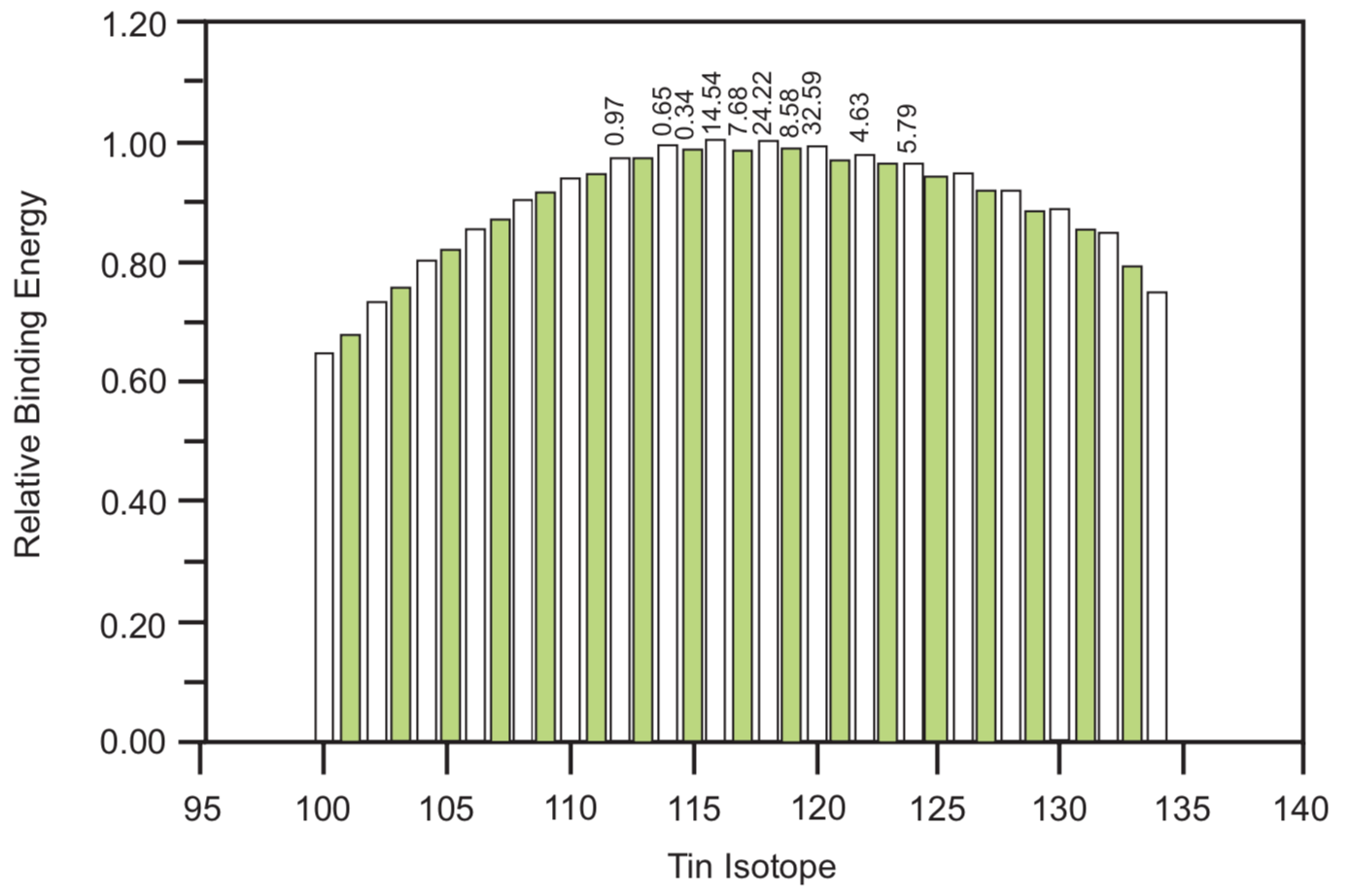
FIGURE 1. Relative Binding Energies of Tin Isotopes. Binding energy for Figures 1, 3 and 5 is taken with respect to the minimum of a smoothed line for a plot of nuclear binding energy vs isotope number. For convenient comparison, the binding energy is normalized to 1.00 for the isotope which has the highest binding energy of the group. Natural abundance percentage designated at the tops of the bars representing stable isotopes. No binding energy data available for tin isotopes 135, 136 and 137.
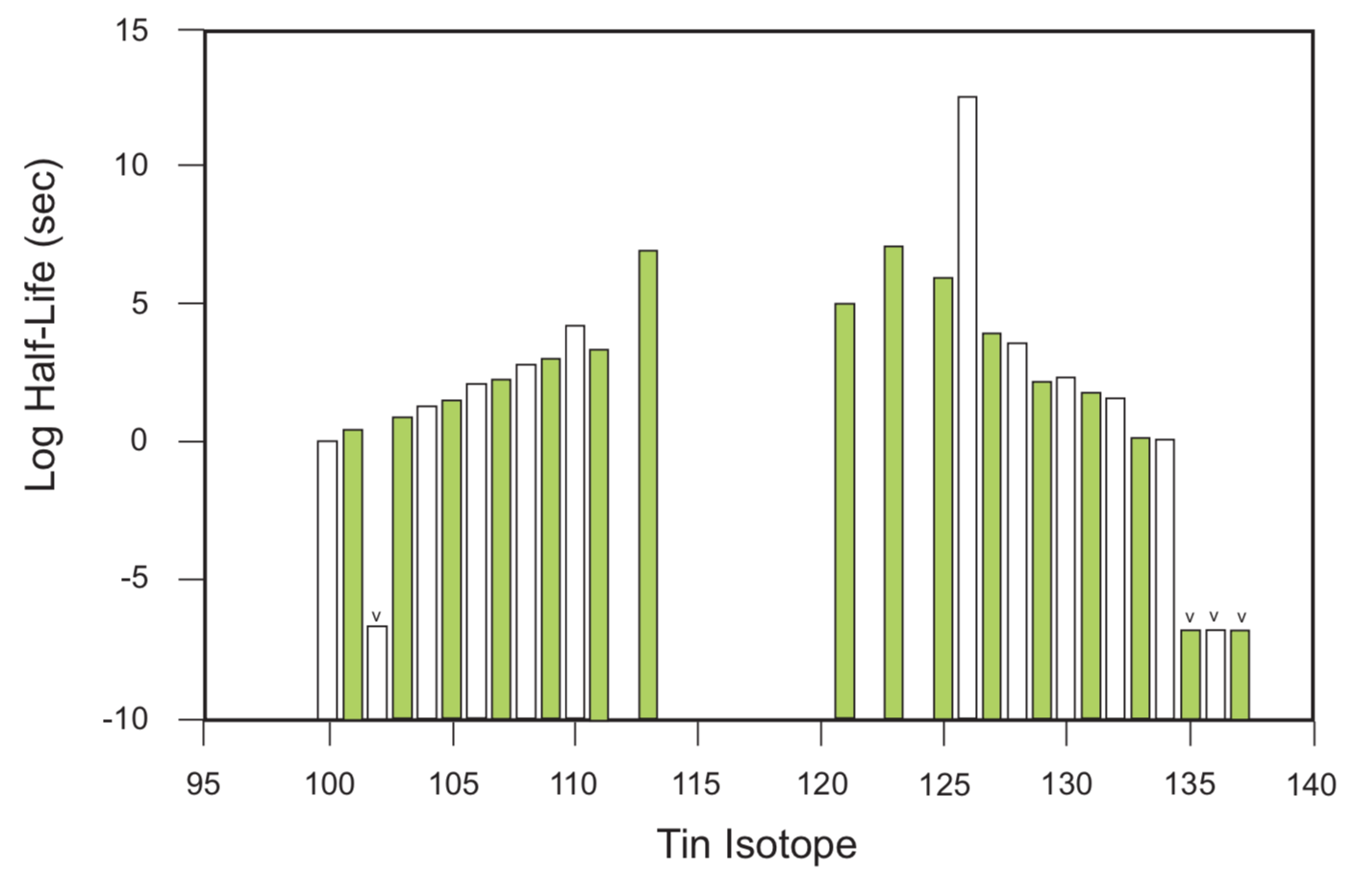
FIGURE 2. Tin Isotope Half-Life. Minimum value of uncertain half-life determination for isotopes 102, 135, 136 and 137 indicated by V.
Similar corresponding data for tellurium are presented in Figures 3 and 4. The half-life of Te-123 is only known to be greater than 1´1013 years (5´1018 min). Although Te-128 and Te-130 are considered to be stable isotopes (abundance 31.687% and 33.799%, respectively), they are weakly radioactive (double-beta decay to xenon 128 and 130), with half-lives 7.7´1024 years and 2.7´1021 years, respectively.
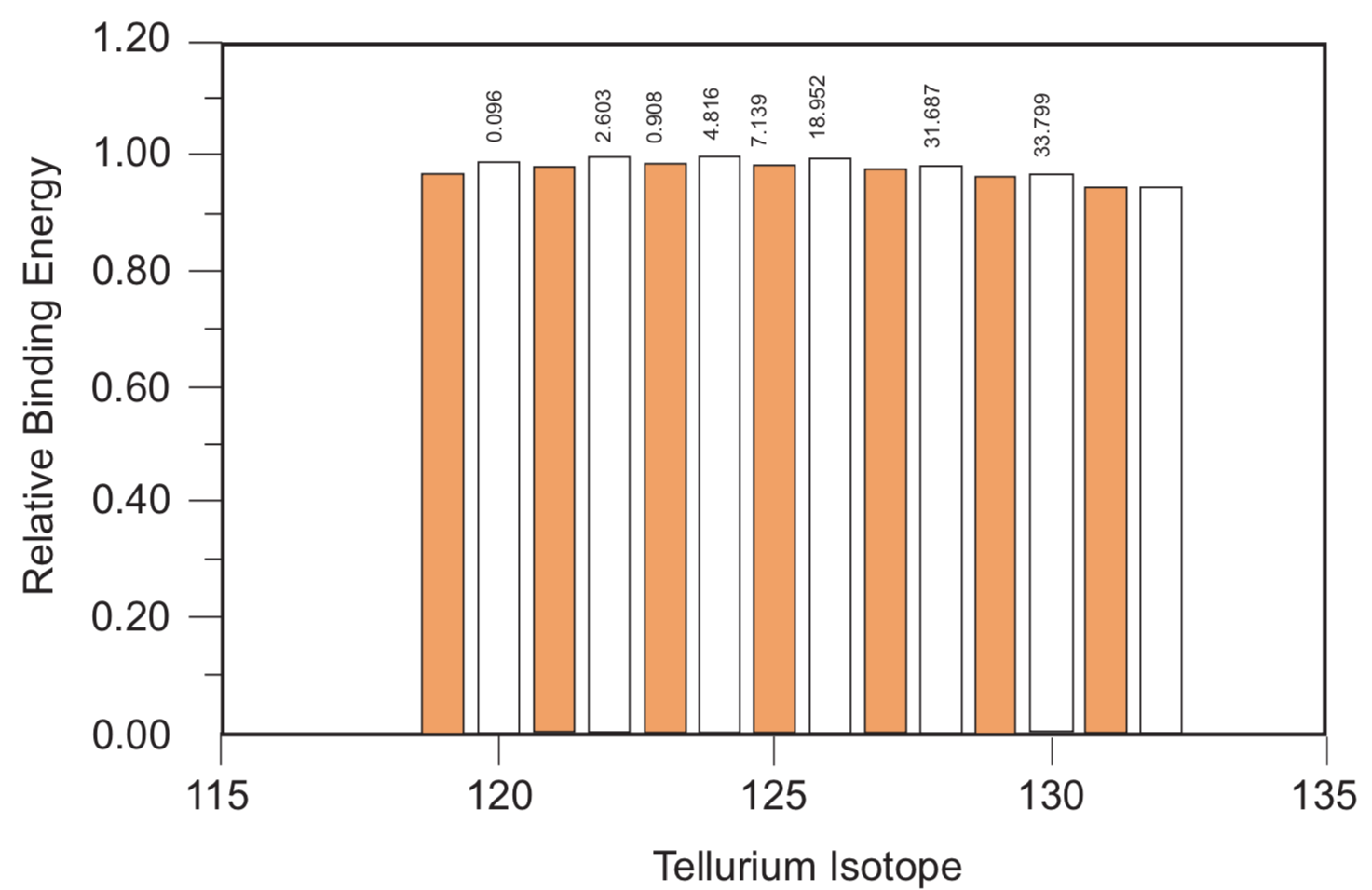
FIGURE 3. Relative Binding Energies of Tellurium Isotopes. Natural abundance percentage designated at the tops of the bars representing stable isotopes.
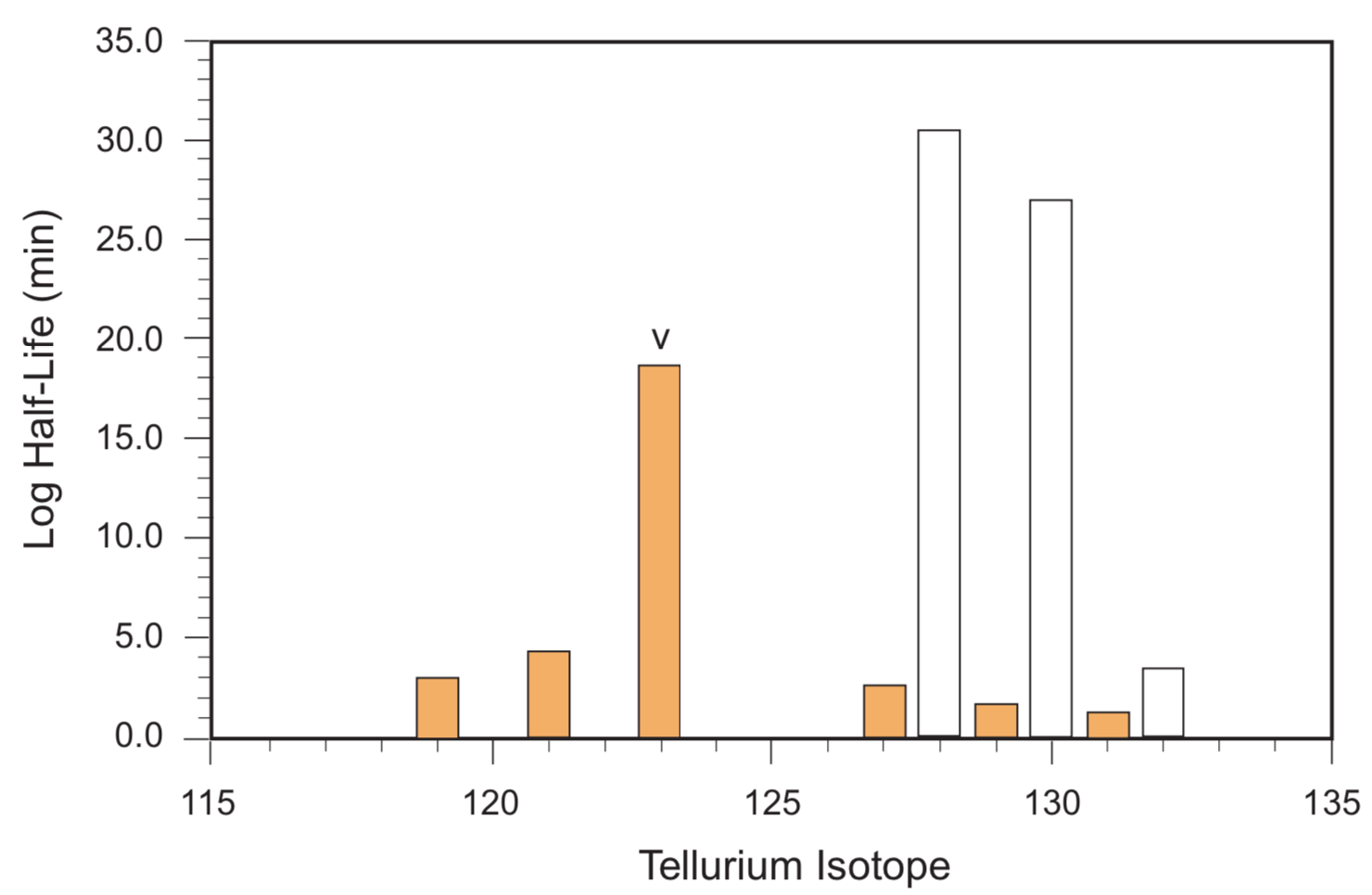
FIGURE 4. Tellurium Isotope Half-Life. Minimum value of uncertain half- life determination for isotope 123.
POLONIUM RADIOHALOS
Since polonium has no stable isotopes, the question arises as to what evidence might be expected for the existence of primordial polonium. Polonium isotopes 199 to 207 decay principally by electron capture in which a proton is changed into a neutron, producing an isotope of bismuth. These bismuth nuclei also capture an electron and convert to an isotope of lead. All the other 20 polonium isotopes decay principally, or entirely, by emission of an alpha-particle (He-4 atom nucleus) to eventually become an isotope of lead. These alpha-particles may damage crystal structure in the surrounding region and produce what are known as radiohalos. Since the damage done by the alpha-particle is greatest at the end-portion of its track, a cross-section through the damaged crystal will show a circle (halo).
The distance an alpha-particle will travel before losing all its kinetic energy will depend on the electron density of the medium in which it is released. Table 1 lists the alpha-track length in standard air for the polonium isotopes 208 through 218. The data in Table 1 were obtained from laboratory measurements on alpha-particles of the same energy as those released by polonium.[4] Conversion of the ranges listed in Table 1 to the corresponding range in a crystal such as mica or fluorite may be estimated to a close approximation by multiplication with the ratio of electron density in standard air to that in the crystal. The average distances traveled in mica for the Po-218, Po-214, and Po-210 alpha-particles are 23.1, 34.4, and 19.5 microns, respectively.[5]Creation's Tiny Mystery[6] contains an excellent collection of radiohalo photographs.
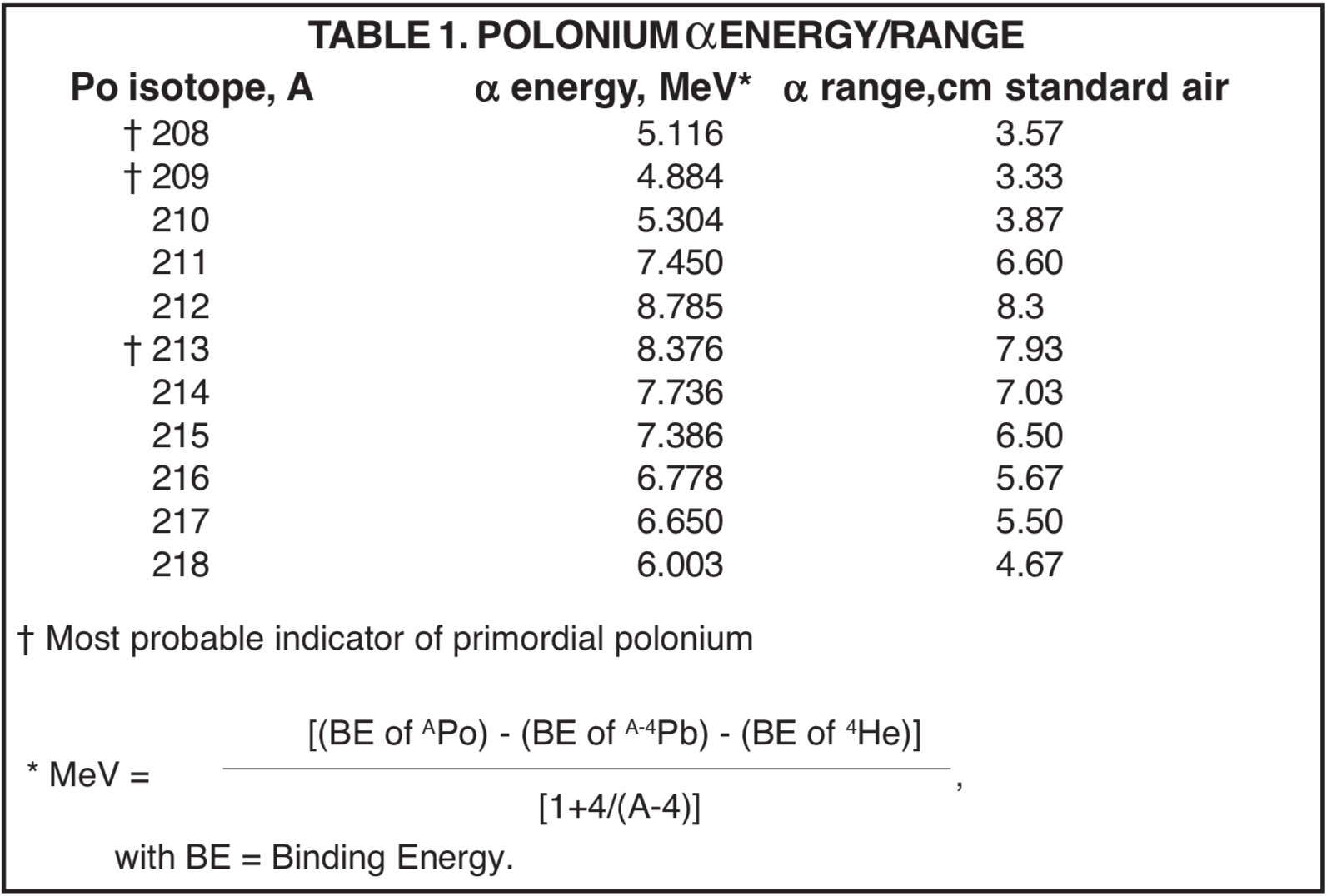
PRIMORDIAL POLONIUM IDENTIFICATION
As indicated in Figures 5 and 6, polonium isotopes 210, 211, 212, 214, 215, 216, and 218 are continually produced by the radioactive decay of thorium and uranium. Only isotopes 208, 209, 213, and 217 in the upper range could be considered uniquely primordial, since there is no other known source for their existence. Any of the polonium isotopes below 199, all of which are alpha emitters, also could provide radiohalo evidence of primordial polonium. The maximum abundance areas in the stable isotope abundance data for tin and tellurium, Figures 1 and 3, suggest that the most likely alpha-emitting primordial polonium isotopes are in the range 208 to 213.
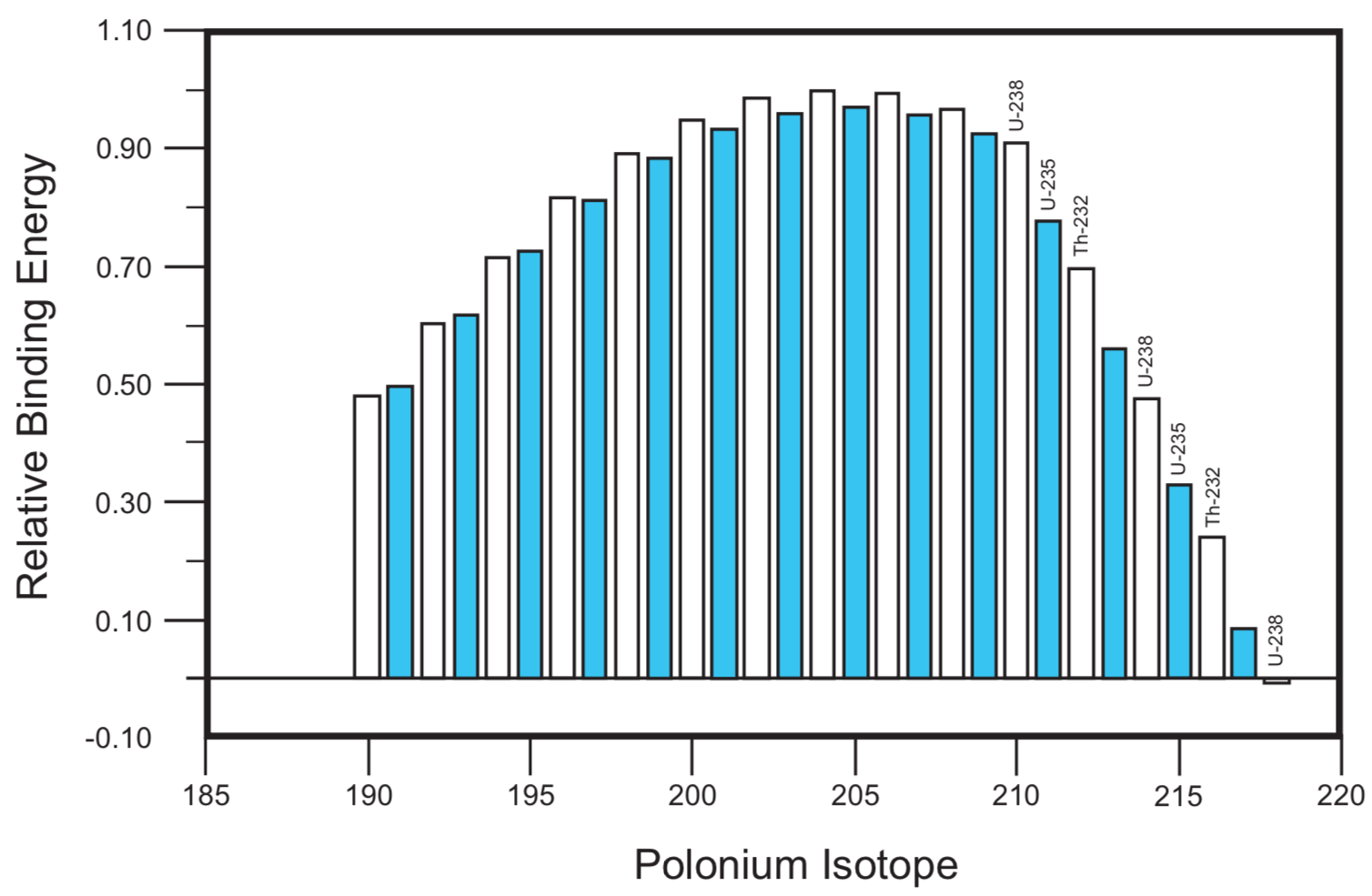
FIGURE 5. Relative Binding Energies of Polonium Isotopes. Long-lived radioactive parent of isotopes associated with radiohalos designated at the tops of the bars for these isotopes.
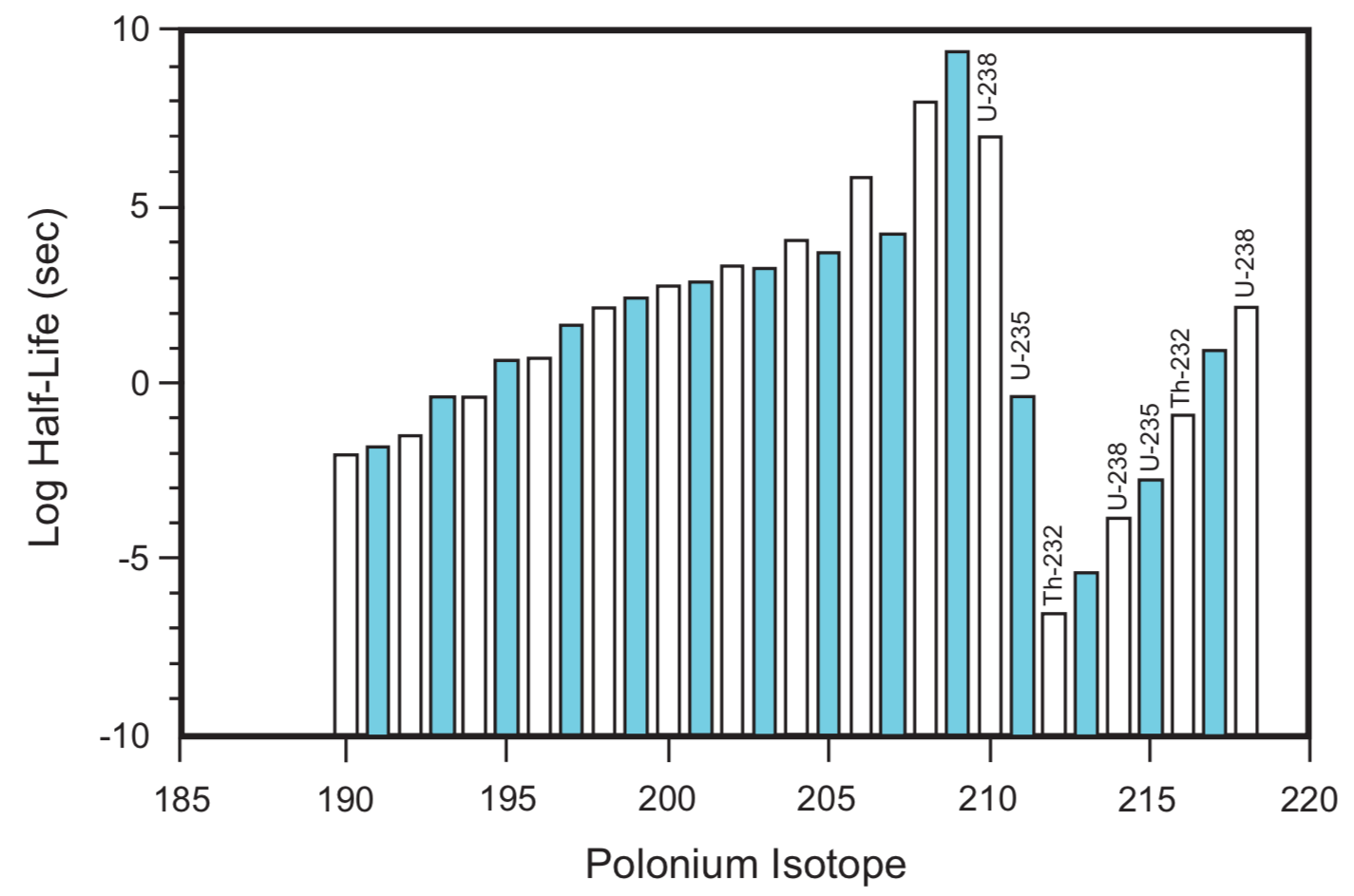
FIGURE 6. Polonium Isotope Half-Life. Long-lived radioactive parent of isotopes associated with radiohalos designated at the tops of the bars for these isotopes.
The data in Table 1 indicate that radiohalos from isotopes 208, 209, and 213 would be readily distinguishable from halos produced by uranium and thorium daughter products. Within the limits of my knowledge, all radiohalos in the 4-9 MeV range reported in the literature are satisfactorily accounted for by uranium and thorium daughters. But consideration must be given to the possibility that some polonium radiohalos that exist today were formed by primordial polonium, rather than by daughters of thorium and uranium.
The longest half-life of the polonium daughters of uranium and thorium is 138.376 days (Po-210, daughter of U-238). Five years after a creation event all primordial polonium of the sort that can be produced also by radioactive decay of a parent would have disappeared.[7] Halos from polonium. isotopes in this category may be interpreted either as having been formed within five years of a primary creation event, or as a consequence of subsequent radioactivity.
A prominent feature of isotope abundance is the predominance of isotopes that have even numbers of both protons and neutrons. This feature is illustrated by the abundance data in Figures 1 and 3. Accordingly, the most abundant isotope of primordial polonium would most likely be the even-even (84 protons, 124 neutrons) isotope Po-208 with a 2.898 year half-life. The stable daughter of Po-208 is Pb-204 (half-life > 1.4´1017 yr), which is 1.4% of common lead. The complete absence of this lead isotope from the central inclusions of some polonium radiohalos[8] clearly indicates that the polonium which formed them was the product of radioactivity rather than primordial creation.
A significant amount of even-odd 102-year isotope 209 would also be expected as a component of primordial polonium. I do not know of any investigation that has reported detection of either Thallium-205, the stable daughter, or Lead-205, the 15.3 million-year radioactive daughter, of Po-209 in the center of polonium radiohalos.
The conspicuous absence of halos associated with polonium isotopes 208 and 209 strongly indicates that the polonium radiohalos which have been observed are a consequence of uranium and thorium radioactivity, and do not provide conclusive evidence of primordial polonium.
THE POLONIUM RADIOHALO ENIGMA
The existence of radiohalos in minerals such as mica has been known since the first decade of the nineteenth century. Efforts to provide an explanation for polonium halos that do not have evidence of a supporting long-lived radionuclide at the halo center (isolated halos) extend as far back as the late 1930s.[5] A halo set produced by 164 microsecond half-life Po-214 (two rings), or by 3.1 minute half-life Po-218 (three rings), without any evidence of a radioactive parent at the site, has been an enigma. The favored explanation has been penetration of a hydrothermal radioactive solution along crystal lattice planes. This explanation readily accounts for the extreme rarity of halos from the six alpha-particles emitted in the decay of thorium to Pb-208, although thorium is over three times more abundant in Earth's crust than is uranium. Thorium and its compounds are relatively insoluble in water, and would not be as easily transported as uranium.
Another enigma is the relative frequencies with which the various types of polonium radiohalos (three rings, two rings, or one ring for the U-238 sequence) are observed.
A clue for finding satisfactory insight into these considerations may be provided by the existence of Po-210 radiohalos in coalified wood from uraniferous sands in the Colorado Plateau.[9] This subfossil wood was evidently buried in the late stages of the Flood, or possibly during a period of intense geological activity in early post-Flood time. Subsurface water carrying highly soluble uranyl ions, together with uranium-series daughter products, evidently infused buried logs. Sites that favored chemical deposition of polonium or polonium precursors accumulated sufficient polonium atoms to produce a detectable polonium halo in the order of 108 atoms, or more.[5]
In a solution containing uranium and equilibrium concentrations of its daughter-products, polonium isotopes 210, 218, and 214 would be present in concentration ratios
[Po-210]/[Po-218]/[Po-214] = 1.000/(1.5´10-5)/(1.3´10-11),
since equilibrium concentrations are proportional to half-life. Infusion into the wood over sufficient time to accumulate enough Po-210 atoms to make only a discernible Po-210 halo site, as in the Colorado specimens, would not deposit enough atoms to produce visible Po-218 or Po-214 halo sites.
To the extent that the intensity of a halo ring is proportional to the number of alpha particles passing through a unit of area, rings from Po-210 daughters of Po-214 may be expected to be 3.3 (range ratio squared) times as intense as rings from Po-214. For polonium deposited from a solution with equilibrium ratios of concentration the corresponding intensity ratio is 73 billion! On this basis complete saturation of crystal damage for the Po-210 ring would occur long before a Po-214 ring became discernible. These considerations raise a question as to why any polonium ring sets occur that have a Po-214 ring without an associated Po-218 ring (Po-214 halos). In an equilibrium state Po-218 is 1.2 million times more abundant than Po-214.
Given a constant supply of Po-218, as is possible from radium, equilibrium ratios among the polonium isotopes would not be reached until about 100 years after a zero-level starting point, because 22.3 year half-life Pb-210 is between Po-214 and Po-210 in the decay sequence (see Figure 7). If the Po-218 input rate is constant, Po-218 and Po-214 will reach equilibrium ratio of 1.1´106 (ratio of half-lives) about 3 hours after a zero-level startup, since 26.8 minute half-life Pb-214 and 19.9 minute half-life Bi-214 are between Po-218 and Po-214 in the decay sequence. During the first few hours of the 100 years required for Po-210 to go from zero-level to equilibrium ratio with Po-218, Po-218 would be more abundant than Po-210 (see Appendix).
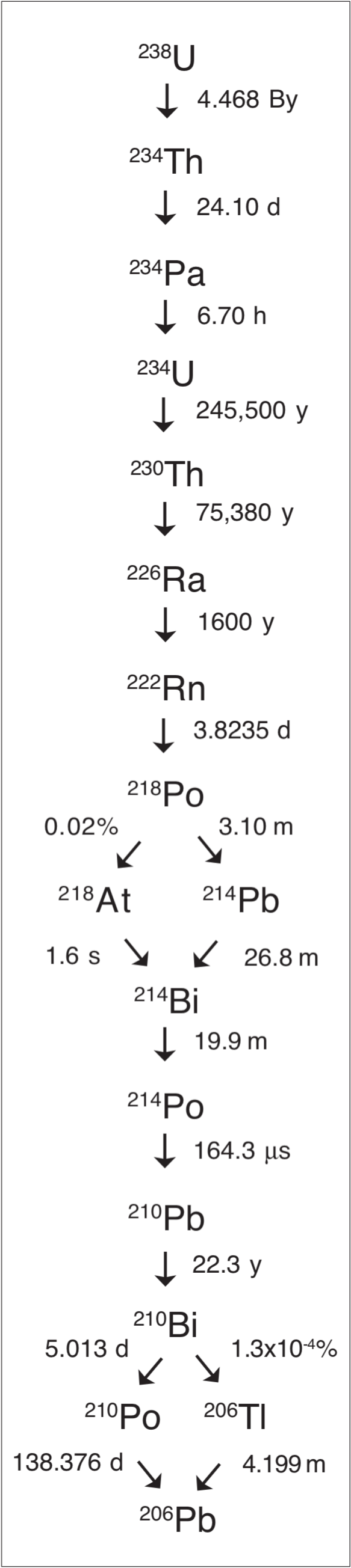
FIGURE 7. Uranium-238 Decay Sequence. Half- life is designated for each stage. Percentage designated for alternate decay routes.
In the natural circumstances in which polonium halos were formed, there probably were large temporal variations in solution flow rates and also isotope concentrations. And there may have been complex geochemical reactions involving polonium, lead, and bismuth. The preceding idealized treatment was provided to indicate parameters within which a logical explanation may be developed for the predominance of Po-210 halos, and for the extreme rarity of Po-214 halos. The chance for a polonium atom finding a binding site in the Colorado fossil wood may have been so low that only Po-210 atoms existed long enough to bind in sufficient numbers to produce a visible radiohalo.
If the infusing solution did not contain a significant amount of radium, any Po-214 and Po-218 that it may have contained would have essentially disappeared within five hours of migration. Polonium-210 that might remain, and Po-210 produced by 22.3 year half-life Pb-210, could be deposited and form Po-210 halos in the wood.
In the development of a model for radiohalos produced by solution infusion, it is important to maintain a distinction between halo density and halo intensity. Density is the number per unit volume of host rock, or number per unit area of field in a viewing microscope. Intensity designates the degree of host crystal deformation in the halo ring, which is related to the number of polonium atoms that produced the halo. Density may relate only to the concentration of sites in the host that are favorable to the deposition of polonium. Intensity is determined by polonium concentration in the infusing solution, infusion rate, and infusion time.
The presence of complete ring sets from Po-218, Po-214, and Po-210 ("Po-218 halos"), and rare double ring sets from Po-214 and Po-210 ("Po-214 halos"), together with predominant single Po-210 rings ("Po-210 halos") in minerals, suggests a fluid-infusion-based separation process similar to that which accounts for the occurrence of only Po-210 halos in coalified wood. A broad study of the relative frequency of Po-210, Po-218, and Po-214 halos in the various minerals in which they may be found, and of the relative intensities of the rings within these halo sets, would be of great value toward resolution of the radiohalo enigma.
The hydrothermal infusion explanation requires that the host mineral lattice contains impurity sites that favor the chemical deposition of polonium or a precursor. Wherever Po-218 is deposited, successive stages in the decay series will produce Po-214 and Po-210, but either of these lighter isotopes could be deposited simultaneously with, or subsequent to, Po-218. Determination of the portion of simultaneous or subsequent deposition could be made by comparison of the intensities of the three rings in the set.[10]
That the postulated hydrothermal infusion process may occur in mica has been fully established. Copper inclusions 0.002 to 0.1 microns thick, and up to 1.0 micron in diameter, are found in favored lattice planes of some biotites.[11] The normal lattice plane separation in biotite is 0.001 micron. Ilton and Veblen have obtained impressive transmission electron microscope images of biotite cross-sections that contain Cu inclusions. The Cu in these inclusions was evidently deposited from a hydrothermal solution. We can expect that similar images for mica containing uranium and polonium radiohalos would show the lead (stable daughter of uranium and polonium) inclusions that x-ray analysis has demonstrated exist at radiohalo centers.[12] The unique Spectacle Halo impressively indicates diffusion of a uraniferous solution across a biotite lattice plane.[13]
The limited knowledge with which we can attempt to model a fluid infusion process, together with selective deposition of polonium isotopes at different sites on the infusion plane particularly the 164 microsecond half-life Po-214 leave "explanations" for radiohalos in an unsatisfactory state. There is a difference of opinion as to whether these halos, particularly those from Po-214 and Po-218, are the direct consequence of a unique creation event, or are the consequence of physical and chemical processes that were established at creation.
When faced with a phenomenon their understanding is unable to comprehend, some individuals who believe in deity as First Cause may form a conclusion as to "how God did (does) it" that way. If a position on the subject is then taken publicly, it is difficult to modify this position when additional evidence indicates that God did it in a different way than they initially thought. It is desirable for all individuals who have taken a position regarding the origin of 164 microsecond polonium halos to hold that position lightly, and in humility, since definitive experimental evidence is limited. The direct creation in situ model readily accounts for some features that have not yet been explained to complete satisfaction by migration of radioactive daughter-products.[14] A model based on infusion of daughter-product solutions accounts for incongruities in the direct creation model.[15]
SUMMARY
As a summary of the observational/experimental evidence, it can be noted that the following considerations favor diffusion of a radioactive solution through crystal lattice planes as an explanation for radiohalos.
- Association of mineral specimens in which radiohalos are found with a region that has a relatively high level of radioactivity.
- The positive relationship between the frequency of radiohalo appearance and the solubility of the radioactive parent(s) associated with the isotope that produced the halo type.
- The positive relationship between the frequency of radiohalo appearance and the half-life of the isotope that produced the halo.
- The restriction of observed halo-producing isotopes to the radioactive daughters of uranium and thorium.
- Complete absence of halos from the most probable primordial isotopes that are not also daughters of uranium and thorium.
- The radiohalo features of uraniferous wood.
- Copper and polonium deposition site patterns on mica lattice planes.
ACKNOWLEDGMENTS
Readers of this treatment are greatly benefited by suggestions from unnamed reviewers whose contributions I am pleased to acknowledge.
ENDNOTES AND REFERENCES
[1]While the nuclear half-life is a quantitative designation only for a statistically large number of toms, it nevertheless is a precise characteristic of the isotope. See: Brown RH. 1990. Radiohalo evidence regarding change in natural process rates. Creation Research Society Quarterly 27(3, December):100-102. Additional comments in CRSQ 28 (4, June 1991):40-41.
[2]1000 years is equal to 9.80 half-lives of 102 years each. (½)9.80 = 0.00112.
[3]Nuclear data in this paper are taken from Nuclear Wallet Cards (5th edition, July 1995). Jagdish K. Tuli, National Nuclear Data Center, Brookhaven National Laboratory, Upton, NY 11973.
[4]Bethe HA. 1950. The range-energy relation for slow alpha-particles and protons in air. Reviews of Modern Physics 22(2):213-219.
[5]Meier H, Hecker W. 1976. Radioactive halos as possible indicators for geochemical processes in magmatites. Geochemical Journal 10:185-195.
[6]Gentry RV. 1988. Creation's tiny mystery. Second ed. Knoxville, TN: Earth Science Associates.
[7]Five years is 13.2 periods of 138.4 day half-life. (½)13.2 = 0.000,107. Po-210 will not reach an insignificant level until its parent 22.3 year half-life Pb-210 does. 13.2 periods of 22.3 years is 294 years.
[8](a) Gentry RV. 1971. Radiohalos: some unique lead isotope ratios and unknown alpha activity. Science 173:727-731; (b) Gentry RV. 1973. Radioactive halos. Annual Review of Nuclear Science 23:347-362; (c) Gentry RV, Cristy SS, McLaughlin JF, McHugh JA. 1973. Ion microprobe confirmation of Pb isotope ratios and search for isomer precursors in polonium radiohalos. Nature 244:282-283.
[9](a) Gentry RV, Christie WH, Smith DH, Emery JF, Reynolds SA, Walker R, Cristy SS, Gentry PA. 1976. Radiohalos in coalified wood: new evidence relating to the time of uranium introduction and coalification. Science 194:315-318; (b) York D. 1979. Polonium halos and geochronology. EOS, Transactions of the American Geophysical Union 60(33):617-618.
[10]If there is no simultaneous or subsequent deposition of the daughter isotopes, the halo density ratios should be approximately inverse to the squares of the halo radii. Simultaneous or subsequent addition of one of the daughter isotopes would make its halo more dense than expected in comparison with the Po-218 ring.
[11]Ilton ES, Veblen DR. 1988. Copper inclusions in sheet silicates from porphyry Cu deposits. Nature 344:516-518.
[12]See Endnote 8c.
[13]The Spectacle Halo is a unique formation of overlapping Po-210 halos. The individual halo centers form a pattern of two circles, one slightly smaller than the other, connected by a tangential straight line. See Endnote 6, Fig. 12 on p 279.
[14]An example is radiohalos in diamond. Armitage M. 1995. Internal radiohalos in diamond. Creation Ex Nihilo Technical Journal 9(1):93-101.
[15]An individual who wishes to pursue this topic further may find the following additional references helpful: (a) Wise KP. 1989. Radioactive halos: geological concerns. Creation Research Society Quarterly 25(4):171-176; (b) Brown RH, Coffin HG, Gibson LJ, Roth AA, Webster CL. 1988. Examining radiohalos. Origins 15(1):32-38.
APPENDIX: POLONIUM ISOTOPE RATIOS
The radioactive solution infusion model requires consideration of isotope ratios during the early stages of solution development. An investigation of the possible values for these ratios can begin with postulation of a solution in which all isotopes below Po-218 in the sequence of Figure 7 are initially at zero concentration, and Po-218 is introduced at rate R to maintain a concentration [Po-218]. When equilibrium is attained each radioactive isotope in the series will decay at rate R. With T representing half-life, R = [Po-218] (ln 2) / TPo-218.
At a constant formation rate, a radioactive isotope will be brought from zero-level to 95% of equilibrium level in 4.322 half-lives. During this time the number of isotope atoms produced will be 4.322T times R. The difference between production and 95% of equilibrium will be conveyed to succeeding isotopes in the sequence. In this example the equilibrium level for Pb-214, the daughter of Po-218, is given by TPb-214 /TPo-218 times [Po-218]. Calculation of the difference between production and 95% of equilibrium yields 17.7 [Po-218].
For Pb-214, 95% of equilibrium will be reached in 116 minutes. If we assume that after 116 minutes Pb-214 is an essentially constant source of Bi-214, Bi-214 will reach 95% of equilibrium 86 minutes later, 202 minutes following start from zero level. In 202 minutes Pb-214 will be at the 99.5% of equilibrium level. This consideration, plus the 17.7 [Po-218] carryover from the first 116 minutes, indicates that Bi-214 will be near 100% of equilibrium by 202 minutes after start from zero level.
Since the equilibration time for Po-214 is negligible in comparison with the half-life of parent Bi-214, the concentration of Po-214 will closely follow that of Bi-214, and all isotopes from Po-218 to Po-214 will be in essential equilibrium at rate R by 200 minutes after beginning of the formation process.
Since the equilibration times for Bi-210 and Po-210 (21 days and 600 days, respectively) are small compared with the half-life of parent Pb-210 (22.3 years), the concentrations of these isotopes will follow the Pb-210 concentration rather closely. At 200 minutes after startup from zero level, Pb-210 will be at only 0.0012% of its equilibrium level for input rate R, and Po-210 will be at the same proportionate level. Since the [Po-210]/[Po-218] equilibrium ratio is 0.667´105, its ratio at 200 minutes is about 0.8.
On the basis of these considerations we can expect a fresh radium solution to have a Po-210/Po-218 ratio less than one for the initial several hours of the time for development of the 6.67´104 ratio that is attained after 100 years.
It is readily apparent from Figure 7 that a site at which there is a deposit of bismuth and/or lead without polonium will not have a Po-218 ring. The only polonium halos in the U-238 sequence that can be produced from deposition at such sites are the Po-214 (two rings) and Po-210 (one ring) varieties. The relative frequency with which Po-214 halos and Po-218 halos are observed may be considered as an indication of the probability for bismuth and lead deposition without polonium.