The geneaologies of Genesis 5 and 11 contain information on birth- and death-dates of a number of patriarchs. It is possible from this information to compute the lifespan of these individuals. When the ages at death are examined for this group, it is found that they present a nonrandom picture in that certain death ages arise with greater frequency than predicted. These results are compared with current demographic data.
A statistical analysis of the chronogenealogies of Genesis 5 and 11 reveals some interesting conclusions.
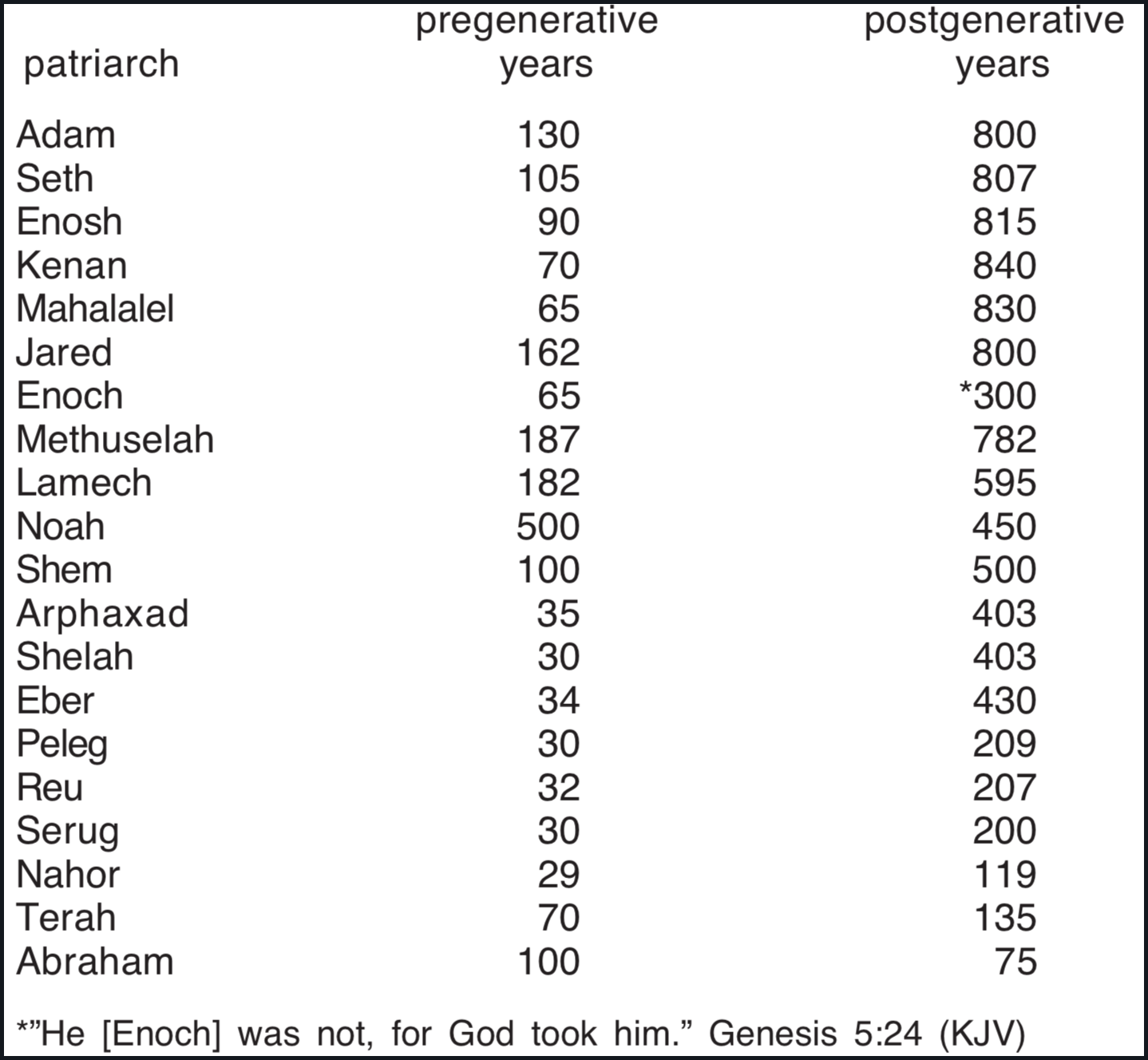
For centuries the genealogies of Genesis 5 and 11 have provided Christians with a chronological framework for history between creation and the time of Abraham. A unique feature of these genealogies is that they record the age of each patriarch at the birth of his presumably first-born son and the number of years the patriarch lived after that event. Genesis 5 additionally records the age of death of each patriarch, this value being the sum of the first two numbers given. In view of these numerical data Genesis 5 and 11 have been called "chronogenealogies" (Hasel 1980a, 1980b).
A persistent use of the Genesis age data has been as a basis upon which to assign a date or an approximate time for the creation. The best-known attempt of this kind was by Archbishop James Ussher in Annales Veteri Novi Testimenti (1650-54). In this work Ussher concluded that creation had occurred during 4004 B.C. While this date was later refined and modified by other scholars, it was to remain the generally accepted date of creation among Christians for two or more centuries (White 1896, pp. 249-256). More recently extensive scientific evidence (Hare 1974, 1979; Abelson 1982) has convinced many Christians that the Genesis age data are unreliable for purposes of chronology (Warfield 1911; Geraty 1974; Horn 1979). However, other Christians argue that regardless of the scientific objections, the most apparent interpretation of scripture (in this case that the genealogies provide an adequate basis for construction of a pre-Abrahamic chronology) stands authoritative (Brown 1977; Hasel 1980b).
With these contrasting opinions in mind we evaluate the Genesis age data without recourse to extrabiblical chronological information. We do not attempt to completely resolve the genealogy/chronology problem, but only demonstrate that these age data form a significantly nonrandom distribution in contrast to an expected random distribution of numbers.
METHODS AND RESULTS
We hypothesized that for any random distribution of pregenerative years (number of years prior to the birth of his first-born son) and postgenerative years (number of years he lives following the birth of his first-born son), the last digits of these values form a random group of numbers. To test this hypothesis questionnaires were sent to staff members of Andrews University asking for birthdates of their fathers and their fathers' first-born sons, and their fathers' death dates.
Thirty-eight questionnaires were returned with complete information. Pregenerative and postgenerative years were calculated for each of the 38 individuals represented. To handle fractions of years consistently the age of the individual at his most recent birthday was used (Bogue 1969, p. 148).
Table 1 shows the pregenerative and postgenerative years of each individual in the control. The frequencies of digits "0" to "9" used as last digits in the pregenerative and postgenerative years, respectively, are shown in Tables 2 and 3. Control frequencies did not vary significantly from expected frequencies (38 numbers / 10 possible last digits = 3.8 in each case) for pregenerative or postgenerative years, confirming our hypothesis that a natural distribution of ages should be random with respect to frequencies of last digits. (Note: The .05 level of significance was chosen for these as well as for the following tests).
TABLE 1. Pregenerative and postgenerative years of 38 fathers of staff members at Andrews University.TABLE 2. Frequency distribution of last digits of pregenerative years of the control sample in Table 1. Observed and expected frequencies are not significantly different (c2 = 4.38, d.f. = 9, P > 0.05).TABLE 3. Frequency distribution of last digits of postgenerative years of the control sample in Table 1. Observed and expected frequencies are not significantly different (c2 = 2.91, d.f. = 9, P > 0.05).
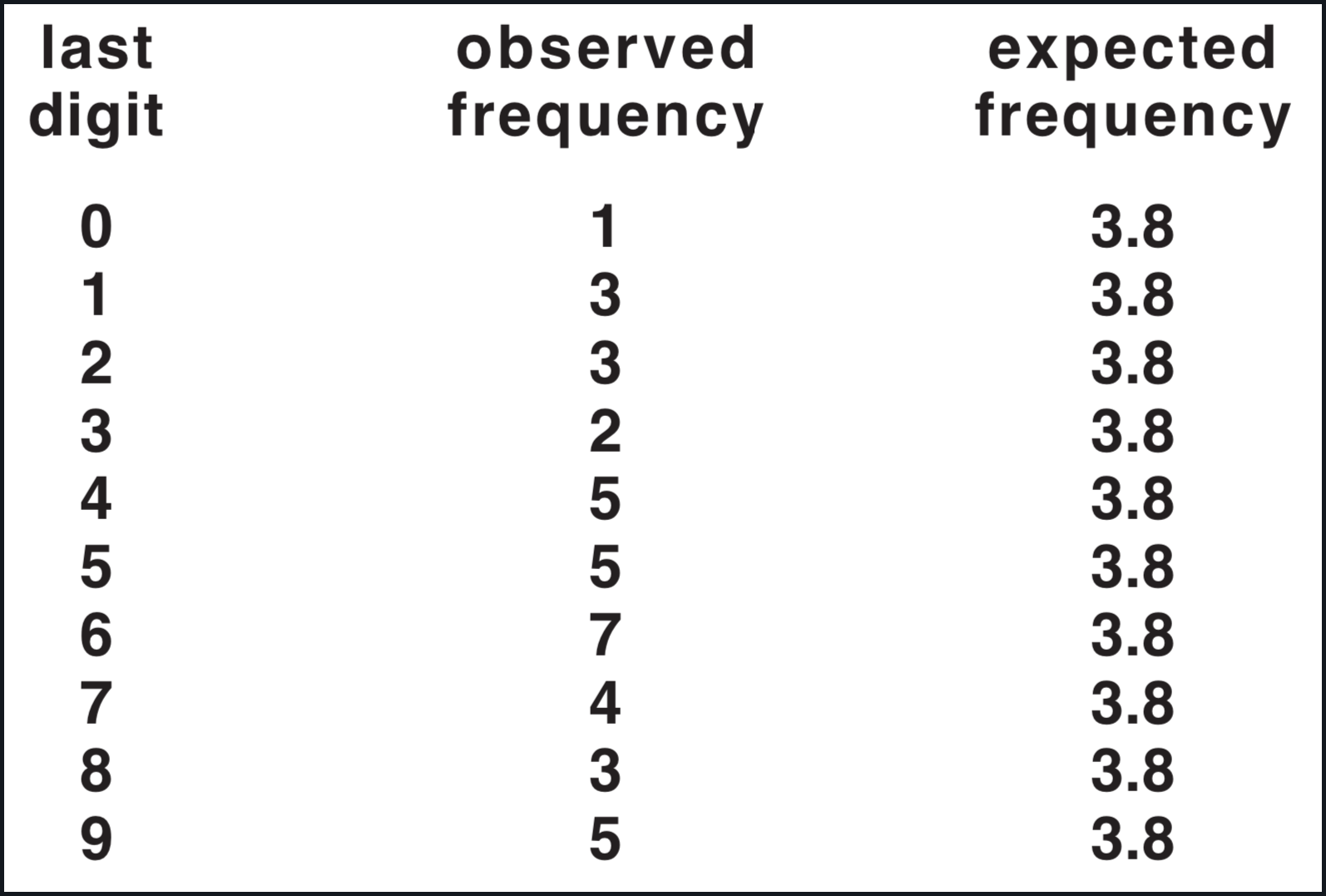
Turning to the data from Genesis 5 and 11 (Table 4) we again hypothesized that the pregenerative and postgenerative year values should be random with respect to last digits. However, the frequencies of last digits of both pregenerative and postgenerative ages show significant deviations from expected frequencies (20 numbers / 10 possible last digits = 2 in each case), implying that the data are biased (Tables 5 and 6).
TABLE 4. The pregenerative and postgenerative years of the 20 patriarchs listed in Genesis 5 and 11 (Masoretic Text).TABLE 5. Frequency distribution of last digits of pregenerative years of the patriarchs listed in Genesis 5 and 11 (Table 4). Observed and expected frequencies are significantly different (c2 = 34.25, d.f. = 9, P < 0.0001).TABLE 6. Frequency distribution of last digits of postgenerative years of the patriarchs listed in Genesis 5 and 11 (Table 4). Observed and expected frequencies are significantly different (c2 = 26.88, d.f. = 9, P < 0.005).
An examination of Table 5 reveals that out of the 20 pregenerative ages represented, 10 have as their last digit a "0" and are thus multiples of 10. The frequency of digit "0" varies most from the expected frequency of 2 and thus contributes most to the large chi-squared value. Ages with the last digit of "5" have the second highest frequency of 4. Remaining frequencies are distributed among four other digits. Digits "1," "3," "6," and "8" are not represented in the distribution. An examination of Table 6 reveals a similar pattern for the postgenerative years. These analyses are based upon data from the Hebrew Masoretic text. Data from the Greek Septuagint reveal essentially the same pattern.
DISCUSSION
As the above tests reveal, the probability that the Genesis age data represent a random distribution of age values is extremely low. Several reasons for this biased distribution can be postulated.
A. The numbers could have been generated by the writer or compiler of the genealogies to fit a preconceived number pattern. One of the best-known attempts to support this hypothesis was by Cassuto (1961, pp. 251-254) who showed that each number in Genesis 5 is a multiple of 5 plus 7, the only exception being the death age of Methuselah which is a multiple of 5 plus 14 (or 2 × 7). He postulated that this numerical series was influenced by the sexigesimal number system. Every 5 years equals 60 months. Multiples of 5 years would then be multiples of 60 months. Additions of 7 to multiples of 5 years would be equivalent to saying "somewhat longer than" the multiple of 5 years. However, there seems to be no rationale for the series of numbers required as multipliers of 5 to arrive at the data, unless it is assumed that the numbers are close to the actual age values for the individuals named. Also, Cassuto's scheme works for all the age values in Genesis 5, but not for all the numbers in Genesis 11. [See Hasel (1980b) for reviews of similar numerical schemes].
B. The numbers could reflect a relationship to the Sumerian King List (Barton 1937, pp. 264-272; Speiser 1964, p. 42), the Ammonite Genealogy of the Hammurapi Dynasty (Malamat 1968; Hartman 1972; Wilson 1975), or other such Middle Eastern lists. On the basis of a number of unique qualities of the Genesis genealogies, Hasel (1978) argued that the appearance of any such relationship is superficial. More recently, however, Walton (1981) has demonstrated a possible numerical link between Genesis 5 and the Sumerian King List.
C. The biased age values may be due to digit preferences by those reporting age data. Demographers have shown that people exhibit preferences for ages having certain terminal digits. For example, single-year-of-age data for the 1960 population of the Philippines shows a strong preference for ages ending in "0," with somewhat lesser preferences for ages ending in "5," "2,'' and ''8." Conversely, these data show negative preferences for ages ending in "9," and "1" (Shryock et al. 1971, p. 204).
Our analysis sheds no light on which, if any, of the above explanations actually accounts for the data. It is even possible that more than one such explanation applies. The concept of statistical nonrandomness which we are postulating states only that the numbers appear biased, suggesting that the Genesis genealogical age data fail to provide a defensible basis upon which to construct a precise-pre-Abrahamic chronology of the world.
REFERENCES
Abelson, P.H. 1982. Creationism and the age of the earth. Science 215:119.
Barton, G.A. 1937. Archaeology and the Bible. American Sunday School Union, Philadelphia.
Bogue, D.J. 1969. Principles of demography. John Wiley, New York.
Brown, R.H. 1977. Radiometric age and the traditional Christian view of time. Origins 4(2):68-75.
Cassuto, U. 1961. A commentary on the Book of Genesis. Part 1. Magnes Press, Jerusalem.
Geraty, L.T. 1974. The Genesis genealogies as an index of time. Spectrum 6(1-2):5-18.
Hare, P.E. 1974. The age of the earth: how it changed from thousands to billions of years. Spectrum 6(3-4):17-27.
Hare, P.E. 1979. Geologic time: the scientific evidence and the Genesis record. Spectrum 10(1):12-19.
Hartman, T.C. 1972. Some thoughts on the Sumerian King List and Genesis 5 and 11b. Journal of Biblical Literature 91:25-32.
Hasel, G.F. 1978. The genealogies of Gen 5 and 11 and their alleged Babylonian background. Andrews University Seminary Studies 16:361-374.
Hasel, G.F. 1980a. Genesis 5 and 11: chronogenealogies in the biblical history of beginnings. Origins 7(1):23-37.
Hasel, G.F. 1980b. The meaning of the chronogenealogies of Genesis 5 and 11. Origins 7(2):53-70.
Horn, S.H. 1979. Can the Bible establish the age of the earth? Spectrum 10(3):15-20.
Malamat, A. 1968. King lists of the Old Babylonian Period and biblical genealogies. Journal of the American Oriental Society 88:163-173.
Shryock, H.S., J.S. Siegel, and Associates. 1971. The methods and materials of demography. Vol. 1. U.S. Department of Commerce, Bureau of the Census. U.S. Government Printing Office, Washington, D.C.
Speiser, E.A. 1964. The Anchor Bible. Genesis. Doubleday, Garden City, New York.
Walton, J. 1981. The antediluvian section of the Sumerian King List and Genesis 5. Biblical Archeologist 44:207-208.
Warfield, B.B. 1911. On the antiquity and the unity of the human race. The Princeton Theological Review 9(1):1-25.
White, A.D. [1896] 1960. A history of the warfare of science with theology. Vol. 1. Dover Publications, New York.
Wilson, R.R. 1975. The Old Testament genealogies in recent research. Journal of Biblical Literature 94:169-189.
