Download PDF January 1, 1983

RE: HAYWARD & CASEBOLT: GENESIS 5 AND 11 STATISTICAL STUDY (Origins 9:75-81) by Mitchell P. Nicholaides, Cambden, South Carolina

This interesting study has hardly said the last word. In fact, probably the best explanation for last digit nonrandomness has been overlooked (or, at least, thoroughly obscured under the heading of “digit preferences”).

That explanation is rounding, to a nearby multiple either of 10 or of 5. What could be more likely, when nearly half the last digits are 0 (19 of 40, per Tables 5 & 6) and another 20% are 5 (8 of 40)? Furthermore, the total absence of 1 and 6 as last digits hints at a rounding down to 0 and 5, respectively.

If the numbers in Table 4 had occurred in a modern document (as, for example, figures on an income tax return), rounding would doubtless have been the first explanation to come to mind for last digit nonrandomness. But critical scholarship is ever pushing us to view the early chapters of Genesis as irrational and arbitrary and to prefer explanations which match that presupposition.

In reality, rounding was even more likely in Bible times than now. “The people of Bible times, as in many parts of the East today, thought more in terms of round numbers than we do, and did not demand mathematical exactitude.” [1] It is extremely unlikely that Moses would even attempt, like the modern demographer, “to handle fractions of years consistently” by using “the age of the individual at his most recent birthday” (p 77).

If rounding alone is sufficient to account for the nonrandom distribution of last digits, then nonrandomness of last digits would not imply nonrandomness of the absolute values of the ages themselves. In that case, Hayward and Casebolt have not actually demonstrated that the “age data form a significantly nonrandom distribution” (p 75).

In more precise terms, the study of Andrews University age data showed that “If age data is non-rounded and random, then last digits are random” ([p^q] ⇒ r). This is logically equivalent to its contrapositive, “Ifvst digits are nonrandom, then age data is either rounded or non-random” (~r = [~pv~q]). Thus, if rounding has occurred, nonrandomness of age data is not necessarily implied.

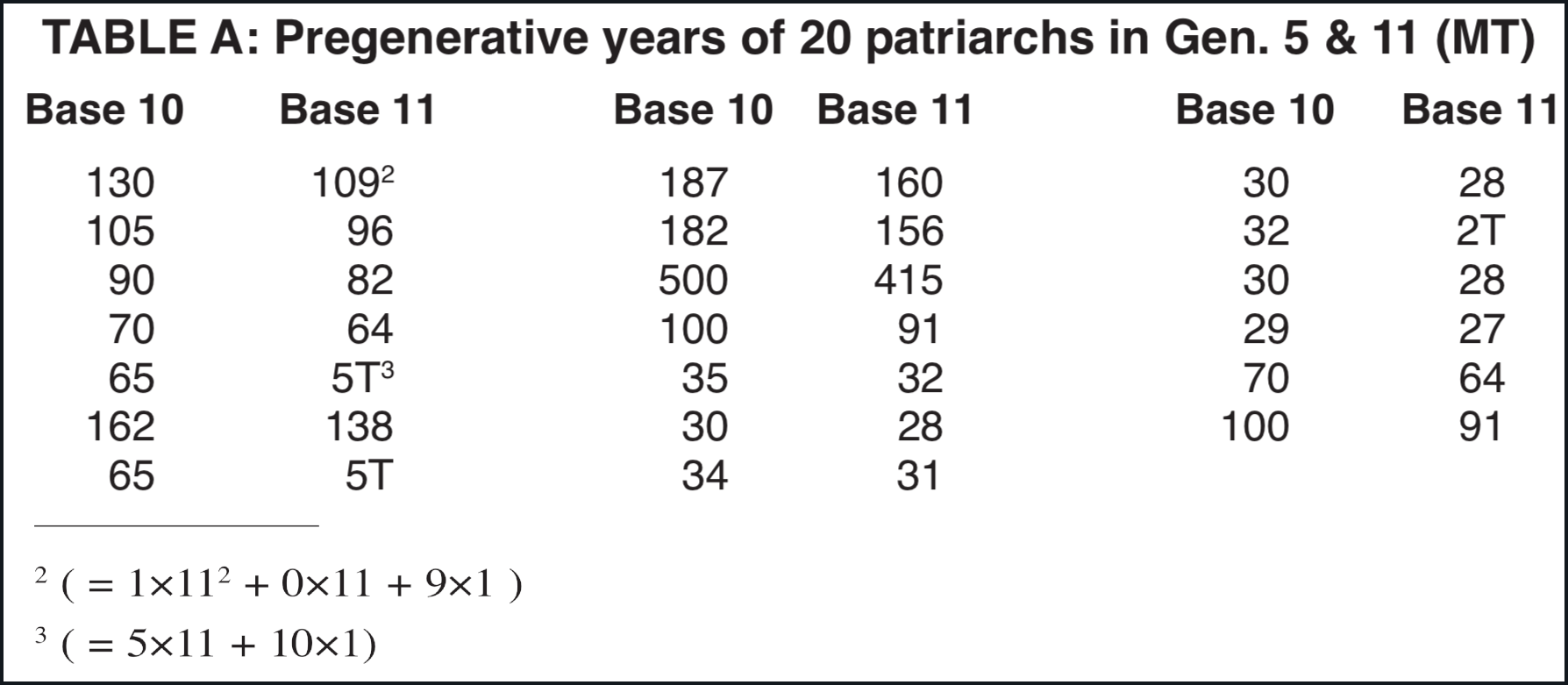
Rounding to a multiple of 10 or of 5 is obviously tied to the base 10 number system. Thus one way of testing whether last digit nonrandomness could be due solely to (base 10) rounding is to change all data to base 11 and see whether last digits then become random. They do — See Tables A and B. (To simplify matters, only pregenerative years are discussed here, since only they are really pertinent to chronology. Results are even more favorable — from my point of view — for postgenerative years.)

Column (a) assumes that one 6 and one 4 had been rounded to the nearest 5, and that three 1’s, two 9’s, and one 8 had been rounded to the nearest multiple of 10. X2 = 7.0, P » 0.05: Observed and expected frequencies are not significantly different. More exactly, P = 0.64±, that is, by chance alone about 2 distributions out of 3 will have observed values that differ even more widely from the expected.

Column (b) represents minimal unrounding to avoid a significant difference. It assumes only that three 1’s and two 9’s had been rounded to the nearest multiple of 10. X2 = 15.0, P > 0.05: Observed and expected frequencies are not significantly different.

What implications would rounding have for the traditional practice of adding the pregenerative age data to calculate the time since creation? If rounding up (e.g., 9 to 10) and rounding down (e.g., 1 to 0) occurred on a roughly equal scale, it makes practically no difference. The rounding per columns (a) or (b) of Table C makes no more than a year’s difference in the time from creation to the birth of Isaac. In the light of the much larger differences in the time periods given by the various ancient texts (LXX, MT, etc.), even a few years difference caused by rounding would be hardly worth mentioning.

I conclude that:

1. Rounding is a totally sufficient explanation and the most likely explanation
   for the observed nonrandomness in the base 10 last digits of the age data of
   Genesis 5 and 11.
2. Such rounding has virtually no effect on the precision of a pre-Abrahamic
   chronology constructed from such age data (— unless one desires an unusual
   degree of precision!).
3. Such last digit nonrandomness is virtually irrelevant to the defensibility
   (whatever that is) of the Genesis chronology.
   Mitchell P. Nicholaides Camden, South Carolina

P.S. Since Seth was not Adam’s “first-born son,” the second sentence of Hayward and Casebolt’s article contains its own sort of “rounding.”

J. L. HAYWARD AND D. E. CASEBOLT REPLY:

We commend Mitchell Nicholaides for his careful statistical analyses and lucidly stated opinions. We heartily agree that our paper “has hardly said the last word” on the topic. As stated in our introduction, “We do not attempt to completely resolve the genealogy/chronology problem.” However, for several reasons we disagree with Nicho- laides’ a priori assertion that “Rounding is a totally sufficient explanation and the most likely explanation for the observed nonrandomness” in the age values, and his implicit conclusion that a meaningful chronology can be constructed from the genealogical data.

First, if rounding of real age values occurred as Nicholaides posits, it did not occur consistently. While 27 of the 40 independent age values are multiples of 5 or 10, 13 are not. Nicholaides’ analysis implies that many digits one number removed from 5 and 10 are rounded. For example, in constructing his Column (a) of Table C he assumes that one 6, one 4, two 9s and even one 8 have been rounded to either 5 or 10. Yet, to choose only two examples (without considering the numbers ending in 2s or 7s) we find that Eber’s and Nahor’s pregenerative ages of 34 and 29, respectively, were not rounded.

Second, deviation from an expected distribution of values in the age data is particu- larly apparent when multiples of 100 are considered. Again, assuming a random distri- bution of frequencies, the expected frequency of multiples of 100 in a series of 40 numbers is less than 1 (40/100 = 0.4). However, examination of our Table 3 reveals that eight (20%) of the 40 independent age values are multiples of 100. (A X2 comparison between the observed and expected values is not too meaningful due to an expected value of less than 1. However, the difference between observed and expected values is so large that statistical testing is unnecessary to evaluate these data.) Those who defend the rounding hypothesis must consider the possibility that not only is a large percentage of the numbers rounded to the nearest 10, but an unnaturally high proportion seem rounded to the nearest 100 as well.

Third, several factors suggest that the writer of the Genesis genealogies was more concerned with style than with chronology. For example, Enoch, the seventh from Adam “walked with God” and was therefore “taken” by God (Genesis 5:22-24). (Also, when he was “taken” he was 365 years old, corresponding to the 365 days of a complete year.) Noah, the tenth from Adam “walked with God” (Genesis 6:9), “won the Lord’s favour” (Genesis 6:8), and during the Flood “only Noah and his company survived” (Genesis 7:23). Abraham, the tenth post-Flood patriarch, was made the father of “a great nation” (Genesis 12:2) with the prediction that “All the families on earth will pray to be blessed as you are blessed” (Genesis 12:3). (All the above quotes are from the NEB.) One searches in vain for mention of comparable benefits accruing to patriarchs of numerically nonsignificant generations. (Of course, other numbers like 3 and 12 held special significance to Hebrew writers, though the patriarchs of corresponding generations did not receive extraordinary blessings. But we think it more than coincidental that each of the patriarchs receiving exceptional recognition by God were members of numerically significant generations.)

Also, the genealogies are neatly organized into two groups of ten patriarchs each, the first group containing antediluvians and the second group containing postdiluvians to the time of Abraham, the father of the Hebrew people. Interestingly, the last patriarch to bear children in each group of ten bore three children, presumably as triplets: Noah fathered Shem, Ham, and Japheth during his 500th year (Genesis 5:32), and Terah begat Abraham, Nahor, and Haran during his 70th year (Genesis 11:26).

Finally, the average pregenerative age of the first nine patriarchs was 116 years, while Noah’s pregenerative age was 500 years, over four times the average. If Noah had had sons at the average pre-Flood age, and if these sons had fathered children at the same average age, and if these children produced descendants of their own at the same average age, and these descendants the same, there would have been an additional three generations of patriarchs alive during the Flood besides Noah and his sons. But, of course, this would have altered the balance the writer achieved by placing ten patriarchs before and ten after the Flood.

The Genesis genealogies would suit well a Hebrew writer’s intent to show ancestral continuity between the Creator God and the Hebrew people, albeit in a somewhat stylistic fashion. But to force Genesis 5 and 11 to assume the role of “chronogenealogies” demands more of scripture than we believe was intended by the inspired writers or is warranted by the evidence.

REFERENCES

[1]Seventh-day Adventist Bible Dictionary, revised edition (1979), p 208.