QUANTUM MECHANICS: THE STRANGE WORLD AT SMALL DIMENSIONS
by
B. L. Clausen Geoscience Research Institute
Science usually uses some kind of model as it tries to make the natural world understandable. It uses the known to model the unknown. This is a standard and useful method, but caution is required when it is necessary to extrapolate from the familiar and understood to the unfamiliar and extreme. Geological and evolutionary models attempt to describe what happened in the distant past history of the earth. Special relativity describes what happens to particles traveling at high speeds close to that of light. General relativity describes the effects of strong gravitational fields. Quantum mechanics describes nature at the extremely small sizes of the atom or nucleus. To demonstrate some of the cautions necessary in developing a model for extreme conditions, it is useful to examine this last model describing small-scale phenomena.[1]
MODELS OF THE INFINITESIMAL
The essence of nature at very small sizes was first discussed by the Greek philosophers Leucippus and Democritus. They believed that discrete, indivisible "atoms" that moved in a void served as the building blocks for matter. The observable world arose from the relation between atoms in the same way that a book arises from the letters that make it up.[2] At one time scientists thought the chemical elements were these fundamental building blocks, then later it was electrons, protons, and neutrons. Now quarks are generally accepted as the particles that make up protons, neutrons, and other exotic particles. This particle nature of matter was extended by Newton to describe light as well. Light as a stream of particles was the accepted model during the 18th century.
On the other hand, Aristotle's physics was the study of nature and its processes on the basis of form and motion.[3] The essence of nature was the action, not the material substance. A medium was needed to initiate and preserve the motion, thus ruling out the possibility of a vacuum. Ocean waves are the action, in contrast to the material substance of the water medium in which they travel. Sound waves are the action in contrast to their medium of air. During the 19th century, the accepted model of light was also a wave model. As a result physicists spent a great deal of time trying to observe the medium in which it traveled and determine its properties. This postulated ethereal substance was called "aether."
In the early 20th century, science developed the quantum-mechanical model to describe the essence of nature at small dimensions that encompasses both the wave and particle concepts. Quantum mechanics has an impressive ability to explain and quantify small-scale phenomena. It was used in developing and explaining such well-known components of our technological society as the television screen, the radio transistor, the computer chip, the grocery-store laser, and the credit-card hologram. Quantum mechanics is the basis for understanding chemistry at the atomic level and for the development of atomic bombs and nuclear power. It has the ability to make exceedingly accurate calculations of the fundamental quantities of nature. According to quantum mechanics, an electron that behaves something like a little magnet should have a magnetic moment that includes a factor of 1.001159655. The experimentally measured value is 1.001159658. This accuracy is equivalent to measuring the distance from Los Angeles to New York to within the width of a blade of grass.[4]
With all its successes, quantum mechanics does not try to answer the question of whether the essence of nature is wave-like or particulate. As a result, it has introduced philosophical issues that have been debated for 60 years.[5] The consequences of the quantum-mechanics revolution have changed the very core of physics and the philosophy of science and are so "shattering as to be almost beyond belief even to the scientific revolutionaries themselves."[6]
THE BEHAVIOR OF LIGHT AS WAVE OR PARTICLE
Light appears to exhibit both wave and particle properties. The wave aspects are evident when light is transmitted from one place to another without losing energy. The wave property of interference accounts for the colors seen in oil slicks, soap bubbles, and peacock wings. The wave property of diffraction accounts for the spreading of light when it passes through a narrow slit. This same wave property explains why water waves can spread around a turn in a river and sound waves can be heard around corners. The particle aspects are important when light interacts with matter during emission and absorption. The model of light as particles or photons is used to explain why light bulbs do not emit ultraviolet radiation and X-rays, why photocells for turning on street lights at night might be more sensitive to blue light than to red light, and why neon and mercury vapor lamps only emit certain colors of light. The particle aspects and the wave aspects of light seem to be important at different times.[7]
Since 1930, quantum mechanics has reconciled these apparently contradictory properties observed for light, but at the expense of introducing some philosophical problems. A laser beam can be used to illustrate the apparent contradictions. The particle model of light must be used to describe the emission of light by the laser. Once the laser "gun" is aimed and the "bullet" particles fired, one should be able to predict where each particle of light will hit the "target" (Figure 1A). It might be expected that a more accurate prediction could be made by passing the beam through a very narrow slit, removing particles at the periphery of the beam. However, after the beam passes the slit it spreads out (Figure 1B), making predictions about any particle less, rather than more, accurate. This spreading of the beam is not at all what would be expected for particles, but is best described by the diffraction property of waves.[8]
FIGURE 1. A laser beam used to demonstrate particle properties (A) and wave properties (B) of light.
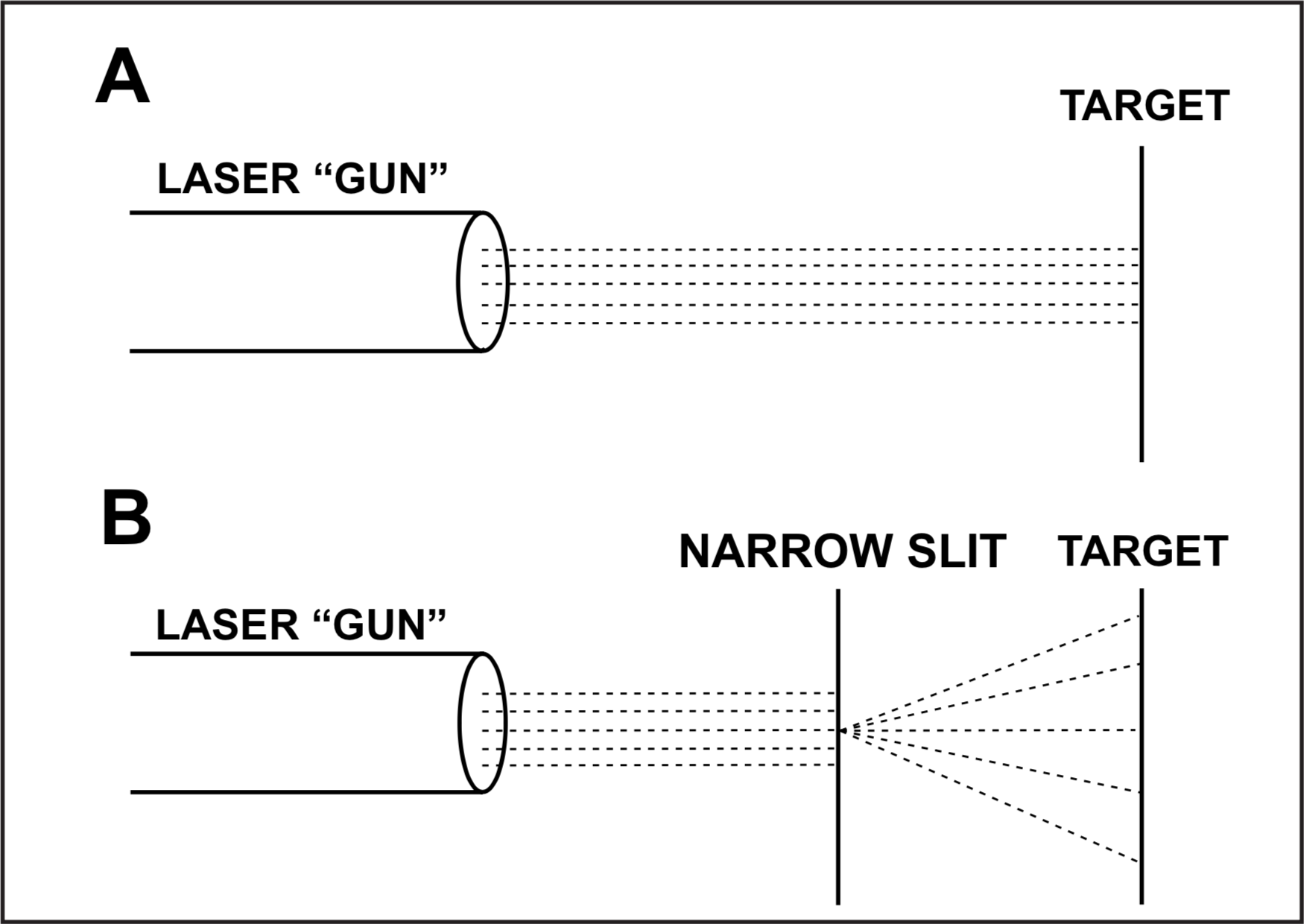
The complementary particle and wave properties of the laser beam demonstrate four philosophical issues introduced by quantum mechanics: (1) One tenet of quantum mechanics, the Heisenberg uncertainty principle, informs us that the more accurately the velocity of the particles aimed at the target is known, the less accurately the position where they hit the target can be known. This is no lack in our physical ability to measure accurately, but is an underlying uncertainty inherent in the natural world. (2) For these small particles, we have lost determinism. The effect (the location where the individual light "particle" hits the target) is no longer completely determined by the cause (the direction the laser-beam "gun" is aimed). (3) The path of any individual particle cannot be predicted. Only a statistical probability can be assigned to each of the many paths possible. The wave diffraction pattern can be described accurately only for a large number of "particles." (4) The experiment determines what will be observed about the behavior of light. Depending on the nature of the experiment, light will behave as a beam of particles traveling in a straight line, or as a wave that spreads after passing an obstacle.
THE BEHAVIOR OF ELECTRONS AS WAVES OR PARTICLES
Like light, the electron sometimes appears to be a particle, and sometimes a wave. It behaves as a particle when it strikes the fluorescent screen of a television picture tube and a small flash of light is produced. However, it can also be diffracted like a wave. In 1907 J. J. Thomson received the Nobel prize for his experimental proof of the particle nature of the electron. In 1937 his son, G. P. Thomson shared the Nobel prize with C. J. Davisson for demonstrating the wave nature of the electron. Father and son demonstrated these two opposite, but complementary, aspects of the nature of matter.[9]
Louis de Broglie was the first to suggest that electrons may exhibit wave as well as particle properties in the same way that light does. Erwin Schrödinger described the motion of the electron in an atom in terms of a wave equation. The complementary particle and wave properties of electrons demonstrate the same philosophical issues as the laser beam: (1) Max Born interpreted atomic electrons as waves by assuming the waves were not real physical oscillations, but probability waves. The size of the wave at any given point in space was related to the probability of finding the electron there. The electron orbit is not a sharply defined circle or ellipse but rather a "cloud of probability density." (2) This interpretation was at the price of certain knowledge: both the location and the speed of the electron could not be described exactly. The relation between these two quantities is expressed in Heisenberg's uncertainty principle. The better known the position of the electron, the more poorly known the velocity and vice versa. (3) The only consistent way to interpret the principle is to assume that the position and speed of an electron is indefinite until an experiment is performed. (4) The uncertainty about present measurements extends to an uncertainty in determining the future. This destroys strict cause-and-effect relations for small-scale phenomena.
At the beginning of the 19th century, Pierre Simon de Laplace argued from the spectacular astronomical successes of Newtonian mechanics that with a knowledge of the total mechanical state of the Universe at any moment of time the entire future would be certain.[10] The uncertainty principle does away with this determinism and strict causality. It only allows the calculation of statistical probabilities for the outcome of any individual small-scale interaction. Only for a large number of atoms or electrons is it possible to make accurate predictions describing their average behavior.
FURTHER CONSEQUENCES OF QUANTUM MECHANICS
According to quantum mechanics, small-scale phenomena include an inherent uncertainty in their measurement, are described by statistical probabilities, are affected by the observer, and are not governed by strict cause-and-effect relationships. Radioactive decay is one of these small-scale phenomena. Quantum mechanics cannot predict exactly when an individual radioactive atom will decay; it can only calculate a probability that the atom will decay in some given amount of time, or calculate an average lifetime for a large number of atoms.
Radioactive decay is affected by being observed. Both the decayed and undecayed state of the atom are inherent until the atom is actually observed. In 1935 Erwin Schrödinger illustrated the situation by a now-famous thought experiment involving a cat.[11] The cat is placed in a box with the following "diabolical device." A small bit of radioactive material is placed in a Geiger counter which, if activated by decay of an atom, win trigger a hammer which shatters a small flask of hydrocyanic acid, killing the cat. According to the rules of quantum mechanics, the total system includes both a live and a dead cat "until someone peeps into the box to check on it, at which point it is either projected into full vitality or else instantly dispatched!"[12] The affect of the observer is still being intensely researched and debated. A recent article entitled "Schrödinger's cat ensnared" describes a 1990 workshop concerned with ways in which quantum-mechanical effects can manifest themselves on a macroscopic scale.[13]
The quantum-mechanical theory of radioactive decay, where the disintegration of any individual atom is random, is in sharp contrast to usual scientific theories that are based directly on cause-and-effect relationships. No two atoms of a radioactive material are the same, because one will decay at one time and another at a different time. It has been suggested in one speculative hypothesis that there may be a cause for the difference. Perhaps the "individual atoms have, in a sense, a memory."[14]
It is well known that, beginning in the 1920s, Albert Einstein broke with the whole of the physics community by refusing to accept quantum mechanics as more than a "provisional" account of nature. He objected to the absence of classical causality and determinism, the introduction of probability as the foundation for physical events, and the consequent incomplete description of nature. Einstein summarized his dislike of these consequences of quantum mechanics in his famous statement, "God does not play dice with the universe." He made numerous attempts to refute the uncertainty principle or to find examples where it would lead to obvious error or paradox.[15] In his most powerful attack on quantum mechanics, Einstein with two other physicists developed a thought experiment now called the Einstein-Podolsky-Rosen (EPR) paradox to show how ludicrous are the consequences of the uncertainty principle.[16]
The EPR paradox has to do with how the act of measurement affects what is observed. Suppose that a particle with no angular momentum decays into two photons. By conservation laws, both photons must have the same polarization. This can be confirmed by placing measuring devices called polarizers perpendicular to the paths of the two photons. If both polarizers are oriented in the same direction ('up' for example) and one photon passes through the polarizer in its path, the other photon will pass through the polarizer in its path, i.e., complete correlation. If the polarizers are arranged perpendicular to each other and one photon passes through the polarizer in its path, the other photon will be blocked by the polarizer in its path, i.e., complete anti-correlation. If the two polarizers are oriented obliquely to each other, the result is intermediate between complete correlation and complete anti-correlation.[17]
According to quantum mechanics, each photon has a combination of potential polarizations after it is emitted. Which potential possibility becomes the reality for each photon has to await a definite measurement or observation, but it takes the measurement of only one particle to effect the reality for both. The problem arises in trying to understand how the well-separated photons can communicate with each other. In particular, if both photons are observed simultaneously, there is simply no time for any signal to propagate between them. Einstein insisted that this result is paradoxical, unless the photons have a distinct polarization at the instant that they separate.In the 1960s, the physicist John Bell studied the theoretical limits on the extent to which such measurements can be correlated.[18] Ben proved that the degree of correlation between the two photons cannot exceed a certain definite maximum, if one assumes as Einstein did that the photons have a definite polarization before they are observed. In contrast, quantum mechanics predicts that this limit can be exceeded. Several experiments were performed to check Bell's inequality, the most notable of which was carried out by Alain Aspect and colleagues at the University of Paris in 1982.[19] The amount of correlation between photons exceeded the maximum that Einstein would have predicted. The strange consequences of quantum mechanics were demonstrated to be correct in contrast to Einstein's "more sensible" interpretations.[20]
The interest is not abating in these philosophical topics of determinism and of the interaction between the observer and the observed. A recent "always-vs-never refutation" of Einstein, Podolsky, and Rosen was described in a 1990 editorial of Physics Today.[21] The topic was addressed by Eugen Merzbacher at an invited talk on "The Raw Nerve of Quantum Physics" in the same year.[22]
CONCLUSIONS
Quantum mechanics is able to account for small-scale phenomena, but only by changing the questions to be asked. The question no longer has to do with whether the actual substance of nature is wave or particle, but with how it is observed to behave. The question has changed from Why does nature behave the way it does? to How does nature behave? Niels Bohr, one of those who worked on developing quantum mechanics, replaced ontological questions such as 'what is light' by phenomenological ones such as 'how does light behave under specified conditions?' Feynman said he could describe how Nature works, but nobody understands why Nature works that way. One can describe the radioactive decay of nuclei, but cannot give a precise cause-and-effect explanation; in contrast to all other areas of science where such changes are precisely what ordinarily would require explanation. The Copenhagen interpretation of quantum events rejects the notion that all changes require explanation.[23]
Basic to the problem is the fact that this theory that applies to the extremes of small size appears to violate common sense. No ordinary objects that we can visualize behave as both particles and waves. Therefore, no large-scale physical phenomena (a) have intrinsic uncertainties in measuring them, (b) disregard cause-and-effect relationships, (c) can only be described in terms of probabilities, or (d) are affected by how they are observed. Niels Bohr resolved the wave/particle contradiction by his complementarity principle. An electron is both a wave and a particle, not a hybrid. Although waves and particles are contradictory concepts for large-scale phenomena, there is no contradiction for small-scale phenomena where the two concepts are complementary. There is no contradiction when it is realized that small-scale phenomena for which we have only indirect evidence cannot be modeled after large-scale phenomena that can be visualized, that are familiar in normal experience, and upon which common sense is based. It is not surprising that no intuitively satisfying model of the small-scale phenomena is possible, because it cannot be based on large-scale phenomena with which we are familiar.
REFERENCES
[1]Gamow, George. 1966. Thirty years that shook physics. Dover Publications, New York.
[2]De Santillana, Giorgio. 1961. The origins of scientific thought: from Anaximander to Proclus, 600 B.C. to A.D. 500. New American Library, New York, pp. 141-146.
[3]Bynum, W. F., E. J. Brown, and Roy Porter (eds.). 1985. Dictionary of the history of science. Princeton University Press, New Jersey, p. 25.
[4]Feynman, Richard P. 1985. QED: the strange theory of light and matter. Princeton University Press, New Jersey, p. 7; see also Halzen, Francis and Alan D. Martin. 1984. Quarks and leptons. John Wiley, New York, p. 162.
[5]Cushing, James T. and Ernan McMullin (eds.). 1989. Philosophical consequences of quantum theory: reflections on Bell's Theorem. University of Notre Dame Press, Indiana.
[6]Cohen, I. Bernard. 1985. Revolution in science. Harvard University Press, Cambridge, Massachusetts, p. 420.
[7]Spielberg, Nathan and Bryon D. Anderson. 1987. Seven ideas that shook the universe. John Wiley, New York, pp. 184-206.
[14]Oliver, Jack. 1991. Solid earth science during the 21st century. Transactions of the American Geophysical Union, EOS 72:121-126.
[15]Mermin, N. David. 1985. Is the moon there when nobody looks? Reality and the quantum theory. Physics Today 38(4):38-47.
[16]Einstein, A., B. Podolsky, and N. Rosen. 1935. Can quantum-mechanical description of physical reality be considered complete? Physical Review 47:777-780.
[17]Davies, Paul. 1983. God and the new physics. Simon & Schuster, New York, pp. 104-106; see also Davies and Brown, p. 16.
[18]Bell, J. S. 1964. On the Einstein-Podolsky-Rosen paradox. Physics 1:195-200.
[19]Aspect, Alain, Jean Dalibard, and Gérard Roger. 1982. Experimental test of Bell's inequalities using time-varying analyzers. Physical Review Letters 49:1804-1807.
[20]d'Espagnat, Bernard. 1979. The quantum theory and reality. Scientific American 241(5):158-181.
[21]Mermin, N. David. 1990. What's wrong with these elements of reality? Physics Today 43(6):9-11.
[22]Merzbacher, Eugen. 1990. The raw nerve of quantum physics. Bulletin of the American Physical Society 35:2357.
