©Copyright 2018 GEOSCIENCE RESEARCH INSTITUTE
11060 Campus Street • Loma Linda, California 92350 • 909-558-4548

ORGANIZATION AND THE ORIGIN OF LIFE
by
John C. Walton
Lecturer in Chemistry
University of St. Andrews,
Fife, Scotland
WHAT THIS ARTICLE IS ABOUT
Dr. Walton points out two major problems associated with the spontaneous origin of life that are not answered by physical theory. First is the matter of producing, on the basis of random activity, highly organized molecules essential to life. Secondly is the problem of developing a self-replicating “living” system that would not degenerate as a result of random molecular activity. In the context of the problems posed, the author then proceeds to evaluate: 1) modern concepts of natural selection, 2) non-equilibrium thermodynamics, 3) the assumption that there is something unique to biological systems, and 4) the concept of a Designer associated with the origin of life. The author feels that the concept of creation permits reconciliation of the data of physics and biology.
MOLECULAR BIOLOGY AND THE FUNDAMENTAL LAWS OF PHYSICS AND CHEMISTRY
Molecular biologists have made remarkable progress in the last few decades towards an understanding of the mechanisms of cell reproduction and metabolism. For example, the Watson-Crick model provides deep insight into the heredity function of DNA and its mechanism of replication. The essential steps of the in vivo chain of events in protein synthesis are also understood at least in outline.
These achievements have encouraged some molecular biologists in the belief that the "secret of life" has been unveiled and that the problem of the origin and continuance of living structures is basically solved. It is frequently asserted in popular texts that cell biology can now be understood entirely in terms of the conventional laws of physics and chemistry [1], or that "no paradoxes had turned up" in the reduction of biology to physics [2]. Crick is one of the most vigorous champions of this view, making the point this way:
... as we learn more about biological organisms, even the simplest ones, it becomes even more inconceivable that they could have just assembled themselves by a random process. So that this really is the major problem of biology. How did this complexity arise?
The great news is that we know the answer to this question, at least in outline [3].
This position has not gone unchallenged. A considerable number of scientists, particularly from the area of theoretical physics and chemistry, have voiced doubt or positive disagreement with the kerygma of Crick. Some of the most eminent and influential theoreticians such as Schrödinger, Wigner, Polanyi and Longuet-Higgins have suggested that we cannot understand the origin and stability of biological structures in terms of the presently known laws of physics. Something of a confrontation has developed between physicists and biologists over this whole question.
Living matter is distinguished from inanimate matter by its organization, function, purpose, adaptability etc., but these concepts are foreign in the physical sciences. These theoreticians suggest that we do not understand at present how to account for some of them, or even how to express them in the language of theoretical physics [4]. One of the clearest thinkers in this area is Pattee, who has outlined the difficulties in objective fashion in a series of papers [5]. It is the concern of physics to find out whether the facts of a given phenomenon can be predicted or reduced to a fundamental theory. Considerable success has been achieved in understanding the structure and organization of stellar systems in terms of gravitational forces, non-living matter in terms of electromagnetic forces, and atomic nuclei in terms of nuclear forces. The fundamental theory which unifies and interrelates all these phenomena is provided by relativistic quantum mechanics. The special structures and organization of living cells do not seem to fit within this framework, and as yet no force or combination of interactions has been recognised which could be responsible for producing their special organization [5].
The fact that some or all cell functions can be duplicated in the test tube using parts isolated from the organism does not solve the problem. It is not doubted that the atoms and molecules making up the cell individually obey the laws of physics and chemistry. The problem lies in the origin and continuance of the highly unlikely organization of these atoms and molecules. The electronic computer provides a striking analogy to the living cell. Nobody doubts that the parts of the computer all obey the laws of mechanics and electronics. Sections of the computer can be detached from the whole and made to perform their function in a "mock up," analogous to the test tube experiments with cell components. The secret of the computer, the key to its performance, lies in the design and highly unlikely organization of the parts which harness the laws of electronics and mechanics. In the computer, of course, this organization was specially arranged by the designers and builders, and the computer continues to operate because of the attentions of service engineers. The problem that molecular biologists and theoretical physicists are addressing is how organization of an even higher order could have arisen spontaneously in living systems and continue to function and develop.
The purpose of this article is to present some of the questions about living matter which theoretical physicists feel cannot be answered by physical theory as it stands now. Two major problems will be considered: the spontaneous origin of self-replicating systems, and secondly, the stability and reliability of reproductive and metabolic functions. Finally, various solutions to these problems proposed by contemporary scientists will be examined.
RANDOM COMBINATION OF BIOMONOMERS AND THE ORIGIN OF A SELF-REPLICATING SYSTEM
The replication mechanism of simple organisms of the present day depends on the cooperation of at least two types of large biopolymers, the proteins (or enzymes) and the nucleic acids. Both these types of macromolecules are made up of linear sequences of biomonomers, the amino acids and nucleotides respectively. Their primary structures and components are shown schematically in Figure 1. Twenty main types of a-amino acids are found in proteins from living matter, which differ from each other in the nature of the group R attached to the central a-carbon atom. A living cell contains several thousand different proteins which are typically a hundred or so amino acid units long. Nucleic acids are made from four different nucleotides which are distinguished by the nature of the heterocyclic base B attached to the sugar molecule; they range from about one hundred to scores of thousands of nucleotides in length.
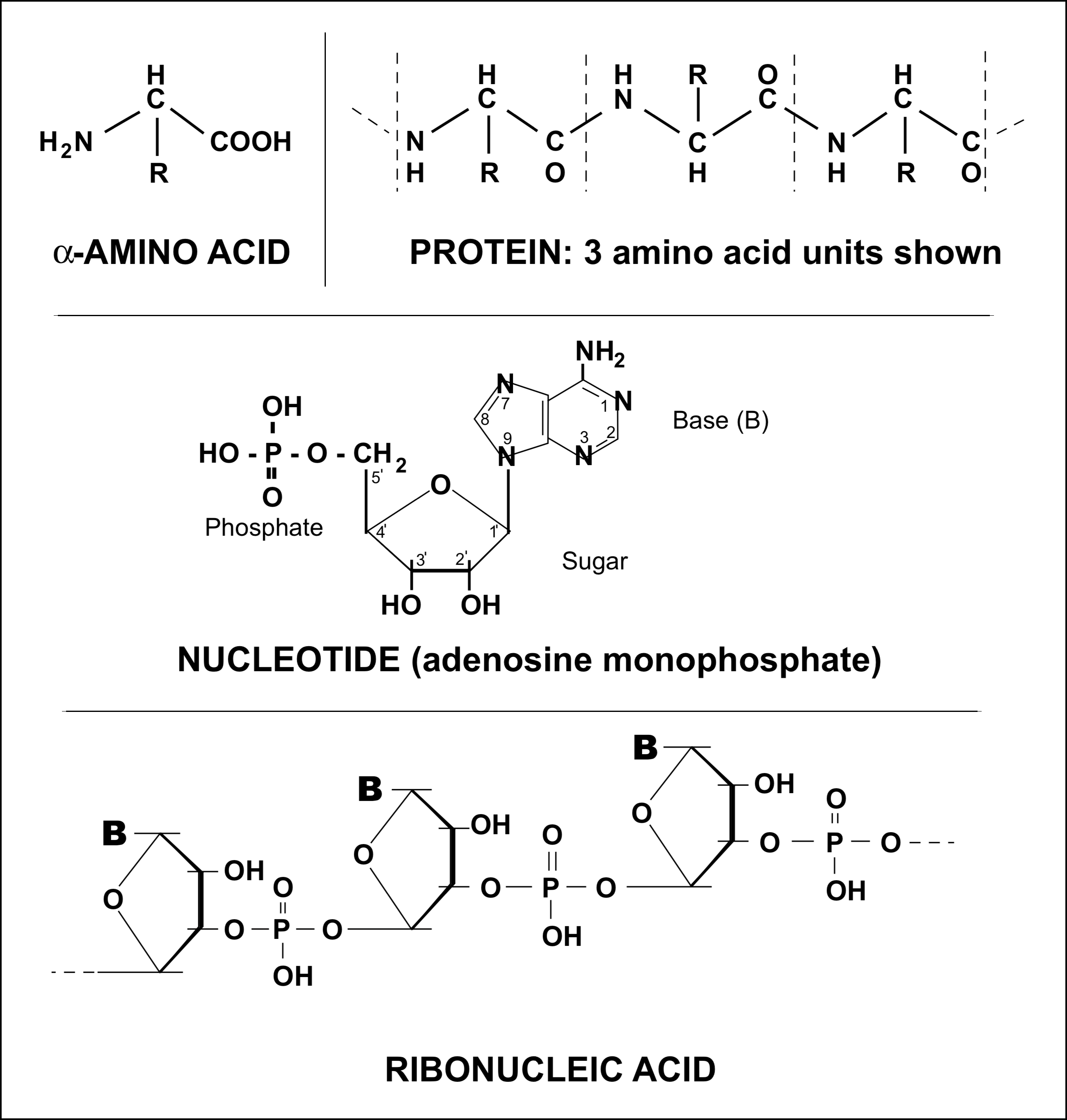
These macromolecules perform highly specific tasks in the replication and metabolism of the organism. It is the exact linear sequence of the amino acids or nucleotides which fits the macromolecule for its particular function. In DNA, for example, the sequence of nucleotides carries the genetic information which is translated into the fabric and organization of the cell. If the sequence is disarranged, then the genetic information is lost, i.e., becomes meaningless on translation. Similarly, it is the sequence of amino acids in an enzyme which defines the secondary and tertiary structure of the macromolecule, and this overall shape enables the enzyme to "fit" the reactants and so act as a catalyst for that specific reaction [6]. Without this precisely defined structure the enzyme loses its specificity towards the substrate and hence its catalytic activity.
Matter, Space and Time Provide Overriding Constraints
The hypothesis that the macromolecules in the first self-replicating system were produced by purely chemical reactions in a large reservoir of biomonomers leads to an impasse. The number of possible sequences of the biomonomers is astronomically high; in other words, the number of macromolecules that could form chemically from the same biomonomers is immense. How could those macromolecules having just the right properties for the start of replication happen to have appeared out of the enormous variety of other possibilities? Some figures are given in Table 1 which illustrate the magnitude of this problem.
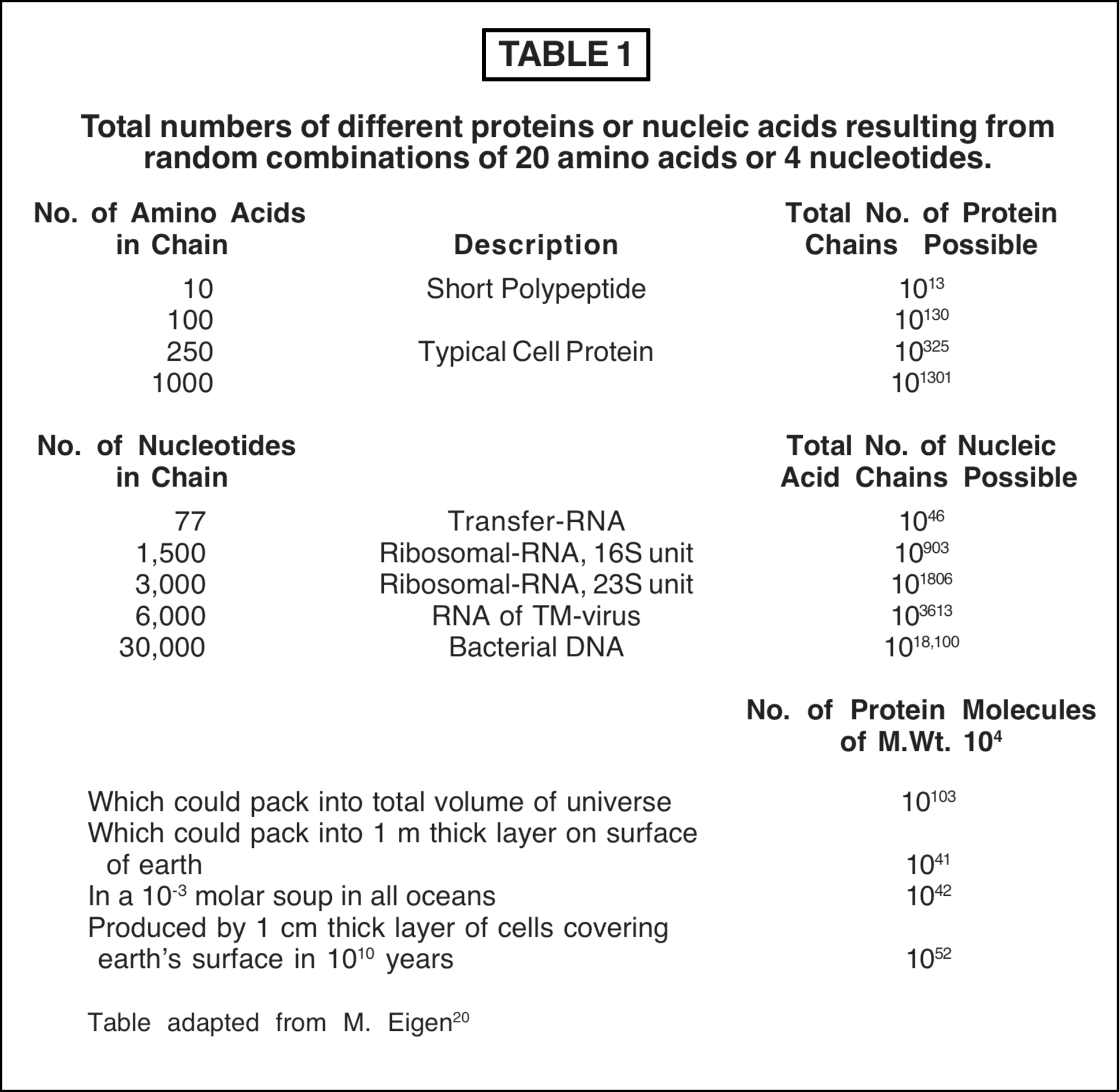
A typical cell protein might contain 250 amino acids, but the number of protein chains which could be formed from the same 250 amino acids is about 10325. A mixture of amino acids combining at random might produce any of these 10325 possibilities and the chance of formation of the particular protein required for a specific reaction in the cell is infinitesimally small. That this is a valid conclusion is shown by the lower panel in Table 1 which gives the numbers of proteins which could occupy various volumes of space. Thus the total number of proteins (M.Wt. 104) which could pack into the volume of the entire universe is only 10103, and the number of proteins which could exist in a 1 metre layer on the surface of the earth or in a "soup" in the ocean is about 1042 or less. These numbers are over 200 orders of magnitude less than 10325 and are almost infinitesimally small in comparison. A rather similar situation prevails for nucleic acids. The number of possible sequences which could be formed by random combination of nucleotides is so large, even for quite short macromolecules (see Table 1), that even if the whole world consisted of a reacting mixture of nucleotides, the chances of formation of any particular sequence required for the first self-replicating organism is effectively zero in one billion (or ten billion) years [7].
The problem is actually more serious than this because chemical reaction of amino acids or nucleotides, unlike the biochemical process, does not necessarily lead to linear sequences of the biomonomers. Some of the amino acids contain acidic or basic groups in the side chain R which can link with other amino acids thus forming branches in the macromolecule. The nucleotides contain reactive positions in the sugar molecule and in the base which can lead to branching or other non-biologic structures. The nucleotides and most of the 20 amino acids also contain chiral centres, so that for each sequence of optically active biomonomers a very large number of stereoisomers could be formed by chemical reactions. In existing self-replicating systems only one of these optically active stereoisomers is effective. When these two factors are taken into account it is apparent that the total number of possible chains given for proteins or nucleic acids in Table 1 represents only a small fraction of the macromolecules that could result from chemical combinations of the monomers.
These fundamental considerations show that there is insufficient space and too little matter in the known universe and that 1010 years, the oft-quoted age of the universe, is not enough time for a self-replicating system similar to known biologic structures to have arisen by purely random chemical combinations.
The Literary Monkey Analogy
An analogy suggested by Cairns-Smith in his thought-provoking book The Life Puzzle illustrates this conclusion most effectively [8a]. A protein molecule can be viewed as a message written in a 20-letter alphabet; and equally a DNA molecule would then represent a message written in a four-letter alphabet. We can consider a message such as: A MERRY HEART MAKETH A CHEERFUL COUNTENANCE, which is written in the 26-letter Roman alphabet, and ask how long it would take a monkey hitting one key per second at random on a 30-key typewriter to produce this 37-letter message. The monkey would hit on a given letter about once every 30 seconds, so the waiting time for the 37-letter message would be 3037 seconds, i.e., about 1052 years. The waiting time for random production of protein or nucleic acid messages consisting of hundreds or more units would be correspondingly longer, and it is clearly out of the question for a universe only 1010 years old [9].
If the monkey were supervised by a "selector" which could recognise the value of each symbol as it was typed and place it in the correct position in the message, then the waiting time could be dramatically reduced. A selector which could recognise words and arrange them in the right sequence could complete the message in less then 6×106 years. And if the selector could pick out each letter as typed by the monkey, the waiting time would be about 20 minutes. Since living organisms containing particular, highly defined messages in protein and nucleic acid manifestly do exist on the earth, some kind of "selection process" must have operated in their construction and organization.
Not only must the selector have been capable of evaluating the potential usefulness of each macromolecule, but it must also have been able to feed back directions to the chemical synthesis process so that the desired products were preferentially formed. This is because purely random synthesis working amongst such an immense number of possibilities could not unaided turn up enough of the required macromolecules. For example, if the entire earth consisted of a-amino acids joined in random 50-unit chains which were mutating at the rate of one amino acid per second, then a 100% efficient selector, which could not influence the mutation process, would only be able to collect about 40 to 50 molecules of one particular 50-unit protein in a period of 5×109 years [8b].
Equilibrium Thermodynamics and the Origin of a Self-Replicating System
A second approach to the problem of the origin of life is provided by the science of thermodynamics. The second law of thermodynamics asserts that the universe is tending towards maximum entropy. The entropy of a system is a measure of the amount of disorder or randomness prevailing in the system. The validity of this law has been demonstrated by numberless empirical experiments and observations, and it finds daily use for correlating and interpreting data from virtually every area of science. The second law of thermodynamics rests in a particularly secure theoretical framework because von Neumann proved it to be a consequence of quantum mechanics [10], and it also finds a striking parallel in the field of information theory [20].
The entire incompatibility of this tendency towards maximum disorder, as observed in physical and chemical processes, with the spontaneous organization of matter into more and more complex hierarchies, as required by the evolutionary theory of the origin of life, has been noted by numerous theoreticians (5, 11, 24, 29).
The laws of thermodynamics are statistical in nature and therefore do not forbid any type of process, but give predictions as to the likelihood or probability of the given process. Some have concluded that although equilibrium thermodynamics indicates high improbability for the spontaneous origin of life, it is not too implausible to suggest that the event might occur in such a long time span as a billion or so years. The thermodynamic calculations published by Morowitz [11] effectively show that this is totally unjustified. Morowitz considers a sample of close-packed living cells which are heated high enough to destroy all chemical bonds and break up the cells into their atomic constituents. The sample is allowed to cool, aged indefinitely, and then subdivided into volumes the same size as the original cells and containing the same atoms. The probability P1 that one of these subdivisions be in a living state was then estimated by two methods based on equilibrium thermodynamics. In the first method an upper limit P1 (max) was calculated from the difference in bond energies of the living state and the ground state. In the second method the free energy of formation of the macromolecular constituents of cells from simple biomonomers, and other organic reactants, was estimated. Some of Morowitz' results are shown in Table 2.
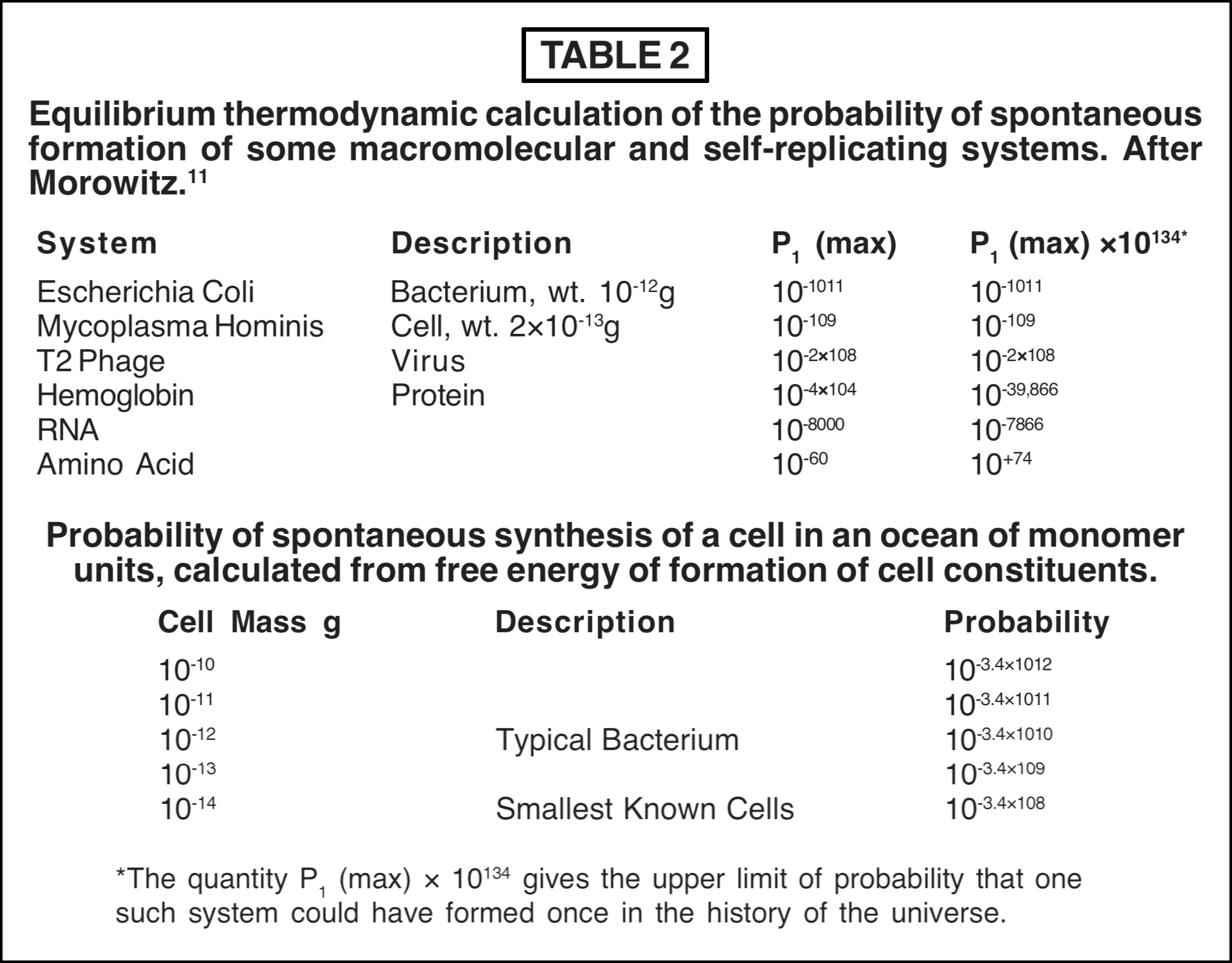
The upper and lower panels give estimates calculated by the two methods, and the agreement between them is very good. The probability of spontaneous synthesis of the smallest cell (or virus) turns out to be unimaginably small in an equilibrium situation. To obtain the probability that a cell (or other structure) would occur spontaneously once in the history of the universe, P1 (max) is multiplied by 10134. This factor is obtained by allowing all the atoms in the known universe (about 10100) to react at the maximum rate of chemical processes (about 1016 sec-1) for a time of 1010 years. However, this factor is negligible in comparison with probabilities as small as 10-1011 and leaves them unchanged. When numbers as infinitesimally small as P1 (max) are encountered, no amount of ordinary manipulation or arguing about the age of the universe or its size can suffice to make it plausible that such a synthesis could have occurred in an equilibrium system [11]. The same type of calculation can also be used to estimate the maximum-sized macromolecule which might be expected as a result of random synthesis. In a mixture the size of the universe, reacting for over a billion years, this turns out to be only a small polypeptide [11].
These calculations illustrate the immense amount of organization that went into the production of the first living system. Equilibrium thermodynamics, like statistical mechanics, points unmistakably to the conclusion that purely random chemical combinations cannot account for the origin of life. In fact this idea has now been almost wholly abandoned (except in elementary texts). It is recognised that some "principle of organization," "selection factor" or "design mechanism" must operate, or have operated, in the past. Crick believes that the necessary organization was the outcome of Darwin's principle of natural selection [3], Morowitz [11], and others, consider that non-equilibrium thermodynamics can supply the answer, Cairns-Smith [8] voices the opinion that self-organization is an inherent property of certain molecular aggregates and macromolecules, Elsasser [12] and Polanyi [13] champion the view that some aspects of biological systems cannot be accounted for in terms of the presently known laws of physics. Before turning to a consideration of these theories of self-organization, we will examine the second problem theoretical physics poses in the field of living structures.
THE RELIABILITY AND STABILITY OF BIOLOGICAL STRUCTURES
A characteristic property of living matter is its ability to reproduce itself virtually without error for an indefinitely large number of generations. Monod lists this reproductive invariance as one of the three general properties of living systems which sets them apart from inanimate matter [14]. The problem that this remarkable reliability and stability presents to physical theory was first clearly set forth by Schrödinger in his fascinating little book What is Life? [15]. The problem has become even more of an enigma as the modern advances in molecular biology have revealed the details of how cell reproduction and metabolism work.
Mechanistic Explanation of Cell Function
Basically the present-day explanation of cell function is a mechanistic one. That is, the molecular components of the cell work in essentially the same way as the mechanical parts of man-made machines. The highly specific function of enzyme catalysis, for example, is understood as the same type of operation to that of a machine tool in a production line. Similarly, the process of replication is compared to a template copying procedure, and the operation of allosteric enzymes in cell control processes is similar to that of a ball-valve or mercury relay.
The almost unlimited reliability of organisms is already remarkable when we compare them with macroscopic machines all of which wear out, wind down, or go wrong. No real system can operate without statistical errors. Even really immense machines such as the solar system wind down eventually because of tidal friction, solar wind effects and so on, but for macroscopic machines in general, the smaller the size and the higher the speed the greater is the error rate (5). The cells of living organisms are incomparably smaller than any man-made machines and yet they function with unprecedented reliability and stability.
Random Motion of Molecules and the Statistical Nature of Physical Laws
This phenomenon becomes all the more striking when it is appreciated that all the properties of living beings are based on a fundamental mechanism of molecular invariance [14]. That is, the components of living machines are molecules. In some organisms the genetic information and the process of replication depend on a single macromolecule; other cell functions depend on collections of molecules containing very few members. Apparently a single molecule, or group of a few molecules, can, in a living system, produce orderly events according to well-defined mechanisms which are highly coordinated with one another and extremely error free. We are faced here with a situation entirely different from that prevailing in the world of physics and chemistry. Individual atoms and molecules in inanimate matter never behave in this way. Outside of biological systems, atoms and molecules undergo random thermal motion so that, even in principle, it is impossible to predict the behaviour of individual particles (except at absolute zero). The only law individual atoms and molecules obey is that of pure chance or random fluctuation. For this reason the fundamental laws of physics and chemistry such as quantum mechanics, thermodynamics, or kinetics are statistical in nature. Thus although individual molecules behave in a random manner, the average effect of an immense number of molecules (say more than 1020 for most macroscopic systems), when acted upon by particular external constraints or boundary conditions, can be a highly exact law.
When a chemist studies the reaction of a very complex molecule he always has an enormous number of identical molecules to handle. He might find that 30 minutes after he had started some particular reaction half the molecules had reacted, and that 30 minutes later three-quarters of them had done so. This kinetic law applies only to the huge collection of molecules; whether any particular molecule will be among those which have reacted, or those that remain, is a matter of pure chance.
Imagine a small amount of powder consisting of minute grains, such as lycopodium, poured onto the surface of a liquid and then observe one of the grains under the microscope. It is found to perform an irregular random motion known as Brownian movement. These grains are sufficiently small to be susceptible to the random impacts of single molecules in the fluid. The motion of a single grain is again unpredictable, but if we have a sufficiently large number of grains the statistical average behaviour gives rise to the well-ordered phenomenon of diffusion.
This is not a purely theoretical speculation; it is not that we can never observe the fate of a single atom or molecule. In the case of radioactive disintegration, for example, it is possible to observe the break-up of individual atoms. It is found, however, that the lifetime of a single radioactive atom is entirely uncertain; it might break-up at any time. The appropriate averaged behaviour of a large collection of identical radioactive atoms results in the exact exponential law of decay.
The most fundamental of all physical theories, quantum mechanics, tells us that this phenomenon of individual indeterminancy reaches even deeper than this. The very components of the molecules themselves, i.e., electrons, protons, neutrons, etc., are not simple particles which work in a mechanistic way like the parts of a machine or miniature solar system. Their regular behaviour can also be described only in a statistical fashion by means of a "wave function" which has to be averaged in the appropriate manner to obtain any given property.
The basic paradox therefore, as Schrödinger realised as long ago as 1944, is this: in inanimate matter regular, orderly behaviour is always the averaged result from a very large collection of molecules acted on by particular constraints. In living matter, however, orderly behaviour appears to result from the activity of single molecules or very small collections of molecules. The fundamental physical laws lead us to believe that single molecules should behave in a random manner and yet in the cell all the hereditary rules are executed with incredible speed and reliability using single molecules.
Modern theoreticians such as Pattee [5] and Bohm [16] have discussed this problem without finding any satisfactory solution. Bohm emphasizes that it is practically certain we cannot understand the transmission of genetic information in terms of fundamental theory and comments on the odd fact that just as physics and chemistry are abandoning mechanistic interpretations, biology is moving over towards them. He concludes:
If this trend continues, it may well be that scientists will be regarding living and intelligent beings as mechanism, while they suppose that inanimate matter is too complex and subtle to fit into the limited categories of mechanism [16].
Some authors attribute the reliability of cell replication to the functioning of the powerful repair mechanisms [3]. This is almost certainly inadequate as an explanation because the physical laws imply essentially random behaviour for single molecules. In addition to this difficulty, the repair mechanism would have to "know" the original structure in order to restore it. If the original molecule under repair were the genetic DNA, the repair mechanism would have to possess, or have access to, another copy of the original. Yet in some organisms the DNA is present in only one or two copies.
Error-correcting devices have been studied in detail by computer theorists amongst whom there is universal agreement that the only way deterioration of the information can be prevented, or at least reduced, is by means of redundancy; that is, the presence of the same information several times over. The lower the desired error rate the greater the number of copies required, and hence the larger the machine [12].
Quantum Mechanical Calculation of the Probability of the Existence of Self-Replicating Systems
Some years ago Wigner [17] also arrived at the conclusion that the reliability of the replication mechanism of living organisms cannot be understood in terms of physical laws. Wigner's approach was a direct application of the quantum mechanical method in a calculation of the probability of the existence of a self-reproducing unit. He considered the interaction of a living system with a nutrient to produce another identical organism, the final state consisting of the two organisms and the remainder of the nutrient. This interaction was assumed to be purely random, i.e., to be governed by a random symmetric Hamiltonian matrix. On counting up the number of equations determining the interaction, he found this greatly exceeded the number of unknowns which describe the final state of the nutrient plus the two organisms. Wigner's analysis showed that it is infinitely unlikely that there be any state of the nutrient which would permit multiplication of the organism. As he puts it, "it would be a miracle" and would imply that the interaction of the organism with the nutrient had been deliberately "tailored" so as to make the lesser number of unknowns satisfy the greater number of equations.
Wigner was careful to point out that his conclusion is not truly conclusive. The most important assumption on which it is based is that the interaction of the nutrient with the organism be governed by a random symmetric matrix. This assumption may, of course, be questioned, but its entire reasonableness is demonstrated by the fact that an identical assumption for the Hamiltonian matrix of complicated systems enabled von Neumann to prove the second law of thermodynamics to be a consequence of quantum mechanics [10].
Landsberg [18] reexamined the application of quantum statistics to the question of the spontaneous generation and reproduction of organisms. Using a different formalism he confirmed that Wigner's assumption leads to practically zero probability for both spontaneous generation and self-replication. If, however, the assumption is broadened to include non-equilibrium systems the probabilities, though small, become greater than zero. So quantum mechanics neither forbids nor excludes the existence of life, but it does suggest that life could not arise or reproduce as a result of the random interactions encountered in inanimate matter. The implication is that some hitherto little understood "principle of organization" must operate in living matter to generate an ordered distribution in which the interaction is somehow "instructed."
CONTEMPORARY THEORIES OF SELF-ORGANIZATION
Neo-Darwinian Natural Selection
The widespread recognition of the impossibility of formation and continuance of self-replicating organisms from purely random combinations has led to a good deal of speculation about the nature of the organizing power or principle which must be involved. Crick, along with many others from the field of biology, considers that the neo-Darwinian mechanism of natural selection provides the answer [3]. A necessary condition for this mechanism is the prior existence of an entity capable of self-replication. Variants are then produced in its genetic material (by mutations for example) and then copied by a passive synthesizing process. Environmental pressures then bring about the dominance of the entities with the greatest probabilities of survival and reproduction.
The weakest point in this explanation of the origin of life is the great complexity of the initial entity which must form by random fluctuations before natural selection can take over. It must carry the information for its own synthesis in its structure and control the machinery which will fabricate any desired copy. What is the simplest entity capable of fulfilling these conditions? Haldane suggested a short polypeptide of low activity and specificity [19], but even this is too complex, because as shown above and as Haldane himself pointed out, the chances of random synthesis of one particular protein are effectively zero. In fact most authors who have considered this question have concluded that neither proteins nor nucleic acids alone possess the requisite properties for self-replication and that a combination of the two types of macromolecules is required [20] [21].
Doubts have also been expressed about the efficacy of the natural selection mechanism itself. There is nothing in neo-Darwinism which enables us to predict a long-term increase in complexity, because greater probabilities of survival and reproduction do not imply greater complexity [22]. Neo-Darwinism also fails to account for the grosser changes of organisms such as epigenesis [22]. Mathematical models of the neo-Darwinian mechanism show that the probability is zero for selection operating in one space (the phenotype) to bring about coherent changes when random mutations are performed in the first space (the genotype) [23].
Non-Equilibrium Thermodynamics and Self-Organization of Matter
Prigogine [24], Morowitz [11] and Eigen [20] [25] have been foremost in the application of non-equilibrium or irreversible thermodynamics, which applies to "open" systems through which energy or matter flows, to the problem of self-organization. In the open part of a system a decrease in entropy or increase in order is possible at the expense of the surroundings. The first essential for an open system is therefore some kind of structured environment.
For example, a gas in a container in contact with a heat source on one side and a heat sink on the other side is an open system, and the simple ordered phenomenon of a concentration gradient is set up in the gas. This order depends for its existence on the structure: source intermediate system sink. If this structure is withdrawn, e.g., if the source is allowed to come into contact with the sink, or if the gas molecules are allowed to diffuse out of the container, the system decays into equilibrium. Another example is a crystal growing in a saturated solution in a container. If liquids are allowed to enter the container or solute molecules to diffuse out, then dissolution of the crystal begins.
The amount of order or organization induced in the open system is a consequence of the amount of information built into the structured environment and cannot be greater than this. Polycondensation of sugars to give polysaccharicles and nucleotides to give nucleic acids can be brought about with the appropriate apparatus (i.e., structure) and supplies of energy and matter. Mora has shown that the amount of order in the final product is no more than the amount of information introduced as physical structure of the experiment or chemical structure of the reactants [26]. Non-equilibrium thermodynamics assumes this structure and shows the kinds of order or organization induced by it. The question of the origin and maintenance of the structure is left unanswered. Ultimately this question leads back to the origin of any structure in the universe, and this is a problem for which science has no satisfactory answer at present [27].
Eigen's development of the application of non-equilibrium thermodynamics to the evolution of biological systems is one of the most comprehensive and far reaching [20] [25]. He showed that the system must be open and far from equilibrium for selection and hence evolution to occur. The reaction must also be autocatalytic in the sense that the product macromolecule must feed back (possibly via some catalytic reaction cycle involving other intermediates) onto its own, and only its own, formation. He recognised that self-organization must start from random events and tried to discover the simplest molecular system which could lead to replication and selection behaviour.
He considered in turn systems containing only nucleic acids, systems containing only proteins, and catalytic networks of proteins and presented detailed and well-reasoned evidence that these are unsatisfactory. The complementary instruction potential of nucleic acids must be combined with the catalytic coupling behaviour of proteins in order to produce the type of structure and function indispensable for a self-replicating organism. This necessitates the presence of molecular machinery for translating the information in the nucleotide sequences into the protein structure. Eigen suggests the "catalytic hypercycle" shown in Figure 2 as the simplest system possessing the requisite properties.
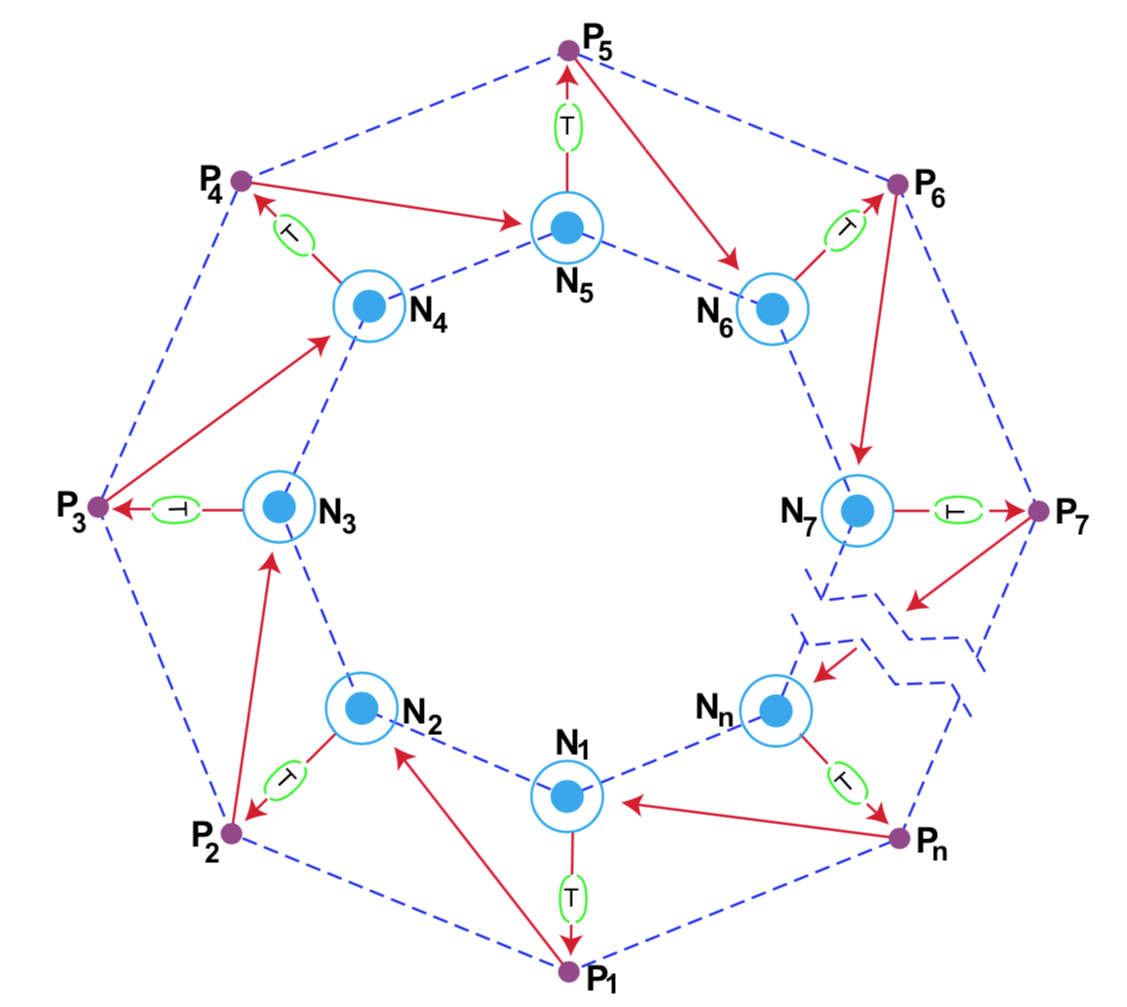
It consists of a number (minimum two) of nucleotide sequences Ni of limited chain length containing the information for one or two catalytically active polypeptide chains Pi. Each polypeptide Pi is coded for by the nucleotide sequence in the corresponding chain Ni which is translated by the molecular machinery (T). The circle around each Ni is a representation of the ability of each nucleotide chain to reproduce itself with the aid of the catalytic enhancement provided by the preceding polypeptide Pi-1. The hypercycle must be closed, i.e., there must be a Pn which can catalyse the replication of the nucleotide sequence N1.
Attractive as the properties of this model are in providing for replication and selection amongst competing hypercycles, there appear to be insuperable problems connected with the formation of the cycle from randomly reacting mixtures of amino acids and nucleotides. Statistical considerations show that the probabilities of formation are effectively zero for the particular nucleotide and protein sequences needed to carry the specific information and catalyse the specific reactions in the hypercycle, especially as they must be produced in sufficient quantities in close spatial and temporal association.
The information in the nucleotide sequence Ni for protein catalyst Pi is made available by the presence of the code translation machinery. This involves several more particular macromolecules (in present-day cells about 50 macromolecules are involved in translation alone). The origin of the genetic code presents formidable unsolved problems. The coded information in the nucleotide sequence is meaningless without the translation machinery, but the specification for this machinery is itself coded in the DNA. Thus without the machinery the information is meaningless, but without the coded information the machinery cannot be produced! This presents a paradox of the "chicken and egg" variety, and attempts to solve it have so far been sterile [14].
Non-equilibrium thermodynamics has been useful in clarifying the essential requirements of structure and energy for organization to develop in molecular systems and in providing new insight into how organisms work. The complexity of Eigen's hypercycle or Cairns-Smith's "evolution machine" [8] and other suggested open systems destroys their credibility as the starting point of molecular evolution.
Biological Structures and "Biotonic" Laws
The impotence of the fundamental physical laws when applied to the origin and operation of biological structures has given renewed impetus to a school of thought favouring the idea that in biology new principles, as yet undiscovered in physics, are needed.
Elsasser has argued for the semi-autonomy of biology from physics on the grounds that the classes of living structures are too small for the statistical averaging procedures of physics to be valid [12]. He coined the term "biotonic laws" to describe the new principles operating in biology. Garstens postulated that a special set of auxiliary assumptions, different from those of physics, would be needed in the application of statistical mechanics to biological phenomena [28]. Polanyi emphasised the mechanism and design in living organisms and their irreducibility to the laws of inanimate matter [13].
Mora finds support for the biotonic law concept in the impossibility of reconciling statistical and thermodynamic constraints with the spontaneous formation of living processes [29]. In addition to the quantum mechanical calculation discussed above, Wigner believes the phenomenon of consciousness points unmistakably to new principles operating in biology [17]. Longuet-Higgins affirms that physics and chemistry are conceptually inadequate as a theoretic framework for biology and recommends thinking about biological problems in terms of design, construction and function [4].
Selection, Organization and Special Creation
A variety of independent applications of the objective laws of theoretical physics to the problem of living organisms, by a disparate series of scientists and philosophers, has disclosed the presence of "selection," "instruction," or "tailoring" in their make-up. Conventional scientific theories of origins have reached a stalemate situation where on the one hand theory and practice show that self-replication is essential for "selection" to occur. But on the other hand, without selection the formation of a self-replicating system is infinitely unlikely. How can this closed loop be broken? Exactly the same situation is encountered with inanimate machines, but here the "selection" or design was supplied from outside by the builders or designers. The indications of design at the molecular level and the analogy from machines are suggestive of external intervention in organisms.
The fundamental postulate of special creation is that living structures were built by an outside agency, i.e., the Creator. The highly unlikely organization of the atoms and molecules in the cell can be reconciled with statistical mechanics if they were deliberately synthesised and arranged by an external agency. The best analogy to this agency that we have is man, and he, working in the laboratory, can synthesise molecules or machines in imitation of nature or of entirely novel formula, which pure chance working with the matter, space and time available on earth could not hope to devise.
The spontaneous generation of biological structures runs counter to the second law of thermodynamics. This contradiction disappears when we consider the structured system: creator material organism, where the organism is an "open" part, like the artifact in the system: man material artifact. A decrease in entropy, i.e., an increase in organization, in the open part of these systems is entirely consistent with the second law.
Wigner's application of quantum mechanics to the replication process implied that "tailoring" of the unknowns to the equations must have occurred in the interaction of the organism with the nutrient. The "principle of organization" at work in this process of instruction might then be identified with the design activity of the creator. It is tempting also to interpret the unprecedented reliability and stability of living organisms to the repair or sustaining activity of the creator. As usual in biology, a mechanical analogy clarifies the situation. Consider an automatic lathe manufacturing a stream of screw-threaded bolts. The uninstructed interaction of the machine with the bolt might take an infinite number of different forms, but the geometry and design of the machine have been tailored so that the cutting tool bears on the bolt for the exact time and with the exact angle and travels the precise distance needed to cut the thread. However, without the constant attention of service engineers the reliability of production would soon deteriorate.
The underlying similarity and unity of biochemical processes imply that life originated only once. The universality of the genetic code and the prevalence of only one optical isomer of biological molecules (such as the L-isomers of amino acids) point to the same conclusion. This is certainly comprehensible in terms of the special creation postulate. Furthermore, the paradox of the origin of the code is removed if the nucleotide sequences were designed and fabricated to couple with the translation machinery and built at the same time. The origin of the code would then be analogous to the origin of Esperanto or Algol.
Outside of the fundamental postulate, special creation violates none of the basic physical laws. It generates none of the contradictions and paradoxes encountered with the molecular evolution hypothesis. It cannot be claimed that creation "explains" the origin and continuance of life. Obviously it transforms the question to one on the nature and continuance of the creator. However, molecular evolution fares no better in this respect, because it simply transforms the question to the origin of structure, matter and energy in the universe.
The postulate of creation of living structures by external intervention undoubtedly restores order, harmony and simplification to the data of physics and biology. At present there is no unambiguous evidence of a scientific nature for the existence of the external entity, but this should not be regarded as a drawback. Many key scientific postulates such as the atomic theory, kinetic theory or the applicability of wave functions to describing molecular properties were, and still are, equally conjectural. Their acceptance depended, and still depends, on the comparison of their predictions with observables. The value of any given postulate lies in its ability to correlate, simplify and organize the observables. Judged by this standard special creation suffers from fewer disadvantages than any alternative explanation of the origin of life.
ACKNOWLEDGEMENTS
The author thanks Dr. C. Mitchell, Dr. S.W. Thompson and Mr. W.G.C. Walton for their invaluable help and encouragement.
FOOTNOTES
J.C. Kendrew. 1967. How molecular biology started. Scientific American 216:142. See also J.D. Watson. 1965. The molecular biology of the gene. W.A. Benjamin, New York, p. 67.
G.S. Stent. 1966. In J. Cairns, G.S. Stent and J.D. Watson, eds. Introduction to Phage and the origins of molecular biology, p. 6. Harbour Laboratory of Quantitative Biology.
F. Crick. 1966. Of molecules and men. University of Washington Press, Seattle and London, pp. 6-7.
C. Longuet-Higgins. 1969. What biology is about. In C.H. Waddington, ed. Towards a Theoretical Biology, vol. 2, p. 227. Edinburgh University Press.
H. Pattee. 1968. The physical basis of coding and reliability. In C.H. Waddington, ed. Towards a Theoretical Biology, vol. 1, p. 67. Edinburgh University Press. See also his other articles in the same journal: 1969. Physical problems of heredity and evolution, vol. 2, p. 268; 1970. The problems of biological hierarchy, vol. 3, p. 117; 1973. Laws, constraints, symbols and languages, vol. 4, p. 248.
There is some evidence that the enzyme may "fit" the transition state of the reaction, rather than the reactants themselves.
See G. Schramm. 1965. Synthesis of nucleosides and polynucleotides with metaphosphate esters. In S.W. Fox, ed. The Origin of Prebiological Systems. Academic Press, London and New York, p. 299.
A.G. Cairns-Smith. 1971. The life puzzle. Oliver and Boyd, Edinburgh, (a) p. 85, (b) p. 34.
Chemical reactions can occur much faster than the "one key per second" rate of the monkey, but even the fastest chemical processes take of the order of 10-16 seconds, which has no significant effect on a time as large as 1052 years.
J. von Neumann. 1932. Mathematische Grundlagen der Quantenmechanik. Julius Springer, Berlin. (English translation: 1955. Princeton University Press, chapter 5).
H.J. Morowitz. 1968. Energy flow in biology. Academic Press, New York and London.
W.M. Elsasser. 1958. The physical foundation of biology. Pergamon Press, New York and London; 1966. Atom and organism. Princeton University Press.
M. Polanyi. 1968. Life's irreducible structure. Science 160:1308.
J. Monod. 1971. Chance and necessity. Translated from the French by A. Wainhouse. Alfred A. Knopf, New York.
E.S. Schrödinger. 1944. What is life? Cambridge University Press, London.
D. Bohm. 1969. Some remarks on the notion of order. In C.H. Waddington, ed. Towards a Theoretical Biology, vol. 2, p. 34. Edinburgh University Press.
E.P. Wigner. 1961. The probability of the existence of a self-reproducing unit. In The Logic of Personal Knowledge. Essays presented to M. Polanyi. Routledge and Kagan Paul, London, p. 231.
P.T. Landsberg. 1964. Does quantum mechanics exclude life? Nature 203:928.
J.B.S. Haldane. 1965. Data needed for a blueprint of the first organism. In S.W. Fox, ed. The Origins of Prebiological Systems. Academic Press, New York and London, p. 12.
M. Eigen. 1971. Self organization of matter and the evolution of biological macromolecules. Die Naturwissenschaften 58:465.
S.L. Miller and L.E. Orgel. 1974. The origins of life on the earth. Prentice-Hall, Englewood Cliffs, New Jersey.
J. Maynard-Smith. 1969. The status of neo-Darwinism. In C.H. Waddington, ed. Towards a Theoretical Biology, vol. 2, p. 82. Edinburgh University Press.
M. Schützenberger. 1967. Algorithms and neo-Darwinian theory. In Paul S. Moorhead and Martin M. Kaplan, eds. Mathematical challenges to the neo-Darwinian interpretation of evolution, p. 73. The Wistar Institute Symposium Monograph Number 5.
I. Prigogine and G. Nicolis. 1971. Biological order, structure and instabilities. Quarterly Review of Biophysics 4:107; I. Prigogine. 1965. Introduction to the thermodynamics of irreversible processes. C.C. Thomas, Springfield, Illinois; P. Glansdorff and I. Prigogine. 1971. Thermodynamic theory of structure, stability and fluctuations. Wiley-Interscience, New York.
M. Eigen. 1971. Molecular self-organization and the early stages of evolution. Quarterly Review of Biophysics 4:149.
P.T. Mora. 1965. The folly of probability. In S.W. Fox, ed. The Origins of Pre-biological Systems. Academic Press, New York and London, p. 39.
See for example E.R. Harrison. 1969. The mystery of structure in the universe. In L.L. Whyte, A.G. Wilson and D. Wilson, eds. Hierarchical Structures. Elsevier, New York, p. 87
M.A. Garstens. 1969. Statistical mechanics and theoretical biology. In C.H. Waddington, ed. Towards a Theoretical Biology, vol. 2, p. 285. Edinburgh University Press; 1970. Remarks on statistical mechanics and theoretical biology, vol. 3, p. 167.
P.T. Mora. 1963. Urge and molecular biology. Nature 199:212.